AdkinsJr
- 148
- 0
Homework Statement
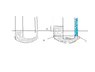
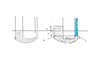
Mercury is poured into a U-tube. The left arm has a cross-sectional area A1=.001 m and the right has A2=.0005m. One hundred grams of water are then poured into the right arm. Determine the length of the water column in the right arm of the U-tube; given the density of mercury is 13.6 g/cm^3, what distance h does the mercury rise in the left arm?
Homework Equations
Just volumes of cylinder and pressure variations with depth:
P=P_o + ρgh
The Attempt at a Solution
I’m not sure how to deal with this problem. I found the height in the column fairly easily since we know the density and mass and cross sectional area, it’s pretty easy to solve for h of the water column, it is .2 meters.
I’m not sure how to set up equations to solve for the distance the mercury has risen though. I don’t know how to apply the principles of static fluids here since there are two different types of fluid.
Pressures are not equal at equal heights I presume. Both surfaces of the water and the mercury must be at the same pressure, atmospheric pressure, yet are at different heights.
However I do think the pressures at points A and B (labeled in the crude scetch) are equal because below the horizontal line I draw there is only mercury.