What happens when two length contracted ladders move through the same garage?

[kmarinas86]

Figure 4: Scenario in the garage frame: a length contracted ladder entering and exiting the garage

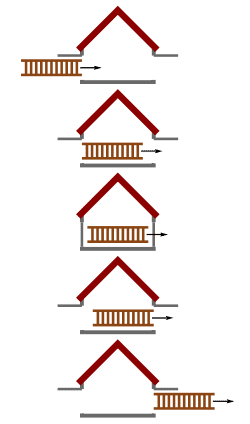
Figure 5: Scenario in the ladder frame: a length contracted garage passing over the ladder

So what happens if we have TWO ladders moving in opposite directions through the same garage?

Figure 4: Scenario in the garage frame: a length contracted ladder entering and exiting the garage

Figure 5: Scenario in the ladder frame: a length contracted garage passing over the ladder

Something's amiss.

How, in the last diagram, does the second ladder (the one faster than garage) spend LESS time inside the garage so that (unlike as depicted in the last diagram) the faster ladder doesn't hit the doors of the garage.

 

[DrGreg]

In Fig 5 you have both ladders entering simultaneously. That's incompatible with them entering simultaneously in Fig 4. (Ditto exiting.)

 

[kmarinas86]

In Fig 5 you have both ladders entering simultaneously. That's incompatible with them entering simultaneously in Fig 4. (Ditto exiting.)

Thanks.