MattRNR
- 1
- 0
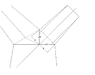
I am having trouble calculating the volume of an unconventional and variable geometric shape (the fork of a tree). I have a conical (frustum) segment which splits and merges at the smaller end into the larger end of 2 smaller conical (frustum) segments and need to calculate the volume of the internal space (using only the length measurements (for each conal frustum), radius measurements (for all 3) and angle measurements (between the middle lines of each of the 2 splitting conal frustums). A diagram (Branching Point) of this should be attached and will make significantly more sense than i do... (Note: i realize in the diagram my radius measurements are a bit displaced but i have the distance of these from the end points and can account for this with a little trigonometry)
Where I am stuck is calculating the volume of the area between the 3 segments, which is infuriating enough on its own, however is further complicated by the problem that (much like the branch of a tree) the two segments may not be the same size nor will the angle between the two segments be constant. Any resultant calculations will have to accommodate for these variables by incorporating them into the equation.
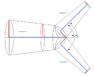
I really am quite stuck here, calculating the volume for each of the conal frustums individually is relatively straight forward, wherein volume can be calculated as [{((π*L)/3)*(R squared + (R*r) + r squared)} where V = Volume, L = Length, R = the largest radius and r = the smallest radius], however for the space in between I'm drawing a blank. The only strategy i can think of is to calculate the volume of the intersection using 4 segments each consisting of a conal frustum that is divided by 2 (this should make more sense in the diagram also (CF method)).
any help you could provide would be greatly appreciated.
Where I am stuck is calculating the volume of the area between the 3 segments, which is infuriating enough on its own, however is further complicated by the problem that (much like the branch of a tree) the two segments may not be the same size nor will the angle between the two segments be constant. Any resultant calculations will have to accommodate for these variables by incorporating them into the equation.
I really am quite stuck here, calculating the volume for each of the conal frustums individually is relatively straight forward, wherein volume can be calculated as [{((π*L)/3)*(R squared + (R*r) + r squared)} where V = Volume, L = Length, R = the largest radius and r = the smallest radius], however for the space in between I'm drawing a blank. The only strategy i can think of is to calculate the volume of the intersection using 4 segments each consisting of a conal frustum that is divided by 2 (this should make more sense in the diagram also (CF method)).
any help you could provide would be greatly appreciated.