Lisa...
- 189
- 0
Hey!
I always had a few difficulties with projectile motion problems, so I just solved one and I wanted to verify if my solution is ok, since I don't have a book with solutions so I can't check if I understood the problem well...
So it's about somebody on a bike who rides off an entrenchment (that's what it's called right?) with a velocity v under an angle of alpha with the ground. He's hoping to land safely on another entrenchement that's h heigher than the first one, at a distance x from the first entrenchment:
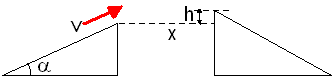
For a given height h, find the minimal velocity vmin the jumper needs to have in order to land safely on the platform at a distance x.
Well what I did is the following:
The well known formula's for the projectile motion are:
x(t)= v0x t + x0
y(t)= y0 + v0y t - 1/2 gt^2
Where v0x= v0 cos @ and v0y= v0 sin @
So if x(t)= x than y(t)= h.
x= v0x t and h= v0y t - 1/2 gt^2
Therefore t= x/v0x. Substitution in the h formula gives:
h= ((v0y x)/v0x)- 1/2 g (x/v0x)^2= ((v0y x)/v0x)- (g x^2)/(2 v0x^2)
Knowing v0x= v0 cos @ and v0y= v0 sin @ substitution gives:
h= ((x v0 sin@)/ v0 cos @) - (g x^2)/ (2 v0^2 (cos^2)@)
h= x tan @ - (g x^2)/ (2 v0^2 (cos^2)@)
(g x^2)/ (2 v0^2 (cos^2)@)= x tan@ -h
(2 v0^2 (cos^2)@)= (g x^2)/ (x tan@-h)
v0^2= (g x^2)/ (2 (cos^2)@ (x tan@ -h))
v0= sqrt((g x^2)/ (2 (cos^2)@ (x tan@ -h)))
Is this correct?! Thanks in advance for your effort!
I always had a few difficulties with projectile motion problems, so I just solved one and I wanted to verify if my solution is ok, since I don't have a book with solutions so I can't check if I understood the problem well...
So it's about somebody on a bike who rides off an entrenchment (that's what it's called right?) with a velocity v under an angle of alpha with the ground. He's hoping to land safely on another entrenchement that's h heigher than the first one, at a distance x from the first entrenchment:
For a given height h, find the minimal velocity vmin the jumper needs to have in order to land safely on the platform at a distance x.
Well what I did is the following:
The well known formula's for the projectile motion are:
x(t)= v0x t + x0
y(t)= y0 + v0y t - 1/2 gt^2
Where v0x= v0 cos @ and v0y= v0 sin @
So if x(t)= x than y(t)= h.
x= v0x t and h= v0y t - 1/2 gt^2
Therefore t= x/v0x. Substitution in the h formula gives:
h= ((v0y x)/v0x)- 1/2 g (x/v0x)^2= ((v0y x)/v0x)- (g x^2)/(2 v0x^2)
Knowing v0x= v0 cos @ and v0y= v0 sin @ substitution gives:
h= ((x v0 sin@)/ v0 cos @) - (g x^2)/ (2 v0^2 (cos^2)@)
h= x tan @ - (g x^2)/ (2 v0^2 (cos^2)@)
(g x^2)/ (2 v0^2 (cos^2)@)= x tan@ -h
(2 v0^2 (cos^2)@)= (g x^2)/ (x tan@-h)
v0^2= (g x^2)/ (2 (cos^2)@ (x tan@ -h))
v0= sqrt((g x^2)/ (2 (cos^2)@ (x tan@ -h)))
Is this correct?! Thanks in advance for your effort!