stunner5000pt
- 1,443
- 4
For a particle of mass m moving in a potential V(r) = -b/r^2 where the constant b>0 obtain the equation r = r(\phi} of the trajectory for the particular states of motion with total energy E = 0 and angular momenta such that \frac{L^2}{2m} < b
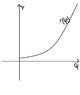
SKetch the trajectory and discuss the motion for
\dot{r} (t=0) >0 and
\dot{r} (t=0) <0
Ok so we know that phi and r are related by this equation
\phi = L \int \frac{1}{r^2 \sqrt{2m(E - V_{e} (r))}} dr + \mbox{constant}
here V_{e} (r) = \frac{-b}{r^2} + \frac{L^2}{2mr^2}
also E = 0 so
\phi = L \int \frac{1}{r^2 \sqrt{2m(\frac{b}{r^2} + \frac{L^2}{2mr^2}}}
and integrating we get
C exp(\phi \frac{\sqrt{2mb - \frac{L^2}{2m}}}{L}}) = r(\phi) = r
so far so good?
for the second part
\dot{r}(t) = \frac{1}{r} \sqrt{\frac{2}{m} (b - \frac{L^2}{2m}}
do i need to find explicit expression for r(t) and phi(t) ?
for r' > 0 then r > 0 and phi > 0
for r' < 0 from the relation between r and phi above it does nt look like that could ever be less that zero unless C <0? Do i need to solve for C by the way?
YOur help is always, greatly appreciated!
SKetch the trajectory and discuss the motion for
\dot{r} (t=0) >0 and
\dot{r} (t=0) <0
Ok so we know that phi and r are related by this equation
\phi = L \int \frac{1}{r^2 \sqrt{2m(E - V_{e} (r))}} dr + \mbox{constant}
here V_{e} (r) = \frac{-b}{r^2} + \frac{L^2}{2mr^2}
also E = 0 so
\phi = L \int \frac{1}{r^2 \sqrt{2m(\frac{b}{r^2} + \frac{L^2}{2mr^2}}}
and integrating we get
C exp(\phi \frac{\sqrt{2mb - \frac{L^2}{2m}}}{L}}) = r(\phi) = r
so far so good?
for the second part
\dot{r}(t) = \frac{1}{r} \sqrt{\frac{2}{m} (b - \frac{L^2}{2m}}
do i need to find explicit expression for r(t) and phi(t) ?
for r' > 0 then r > 0 and phi > 0
for r' < 0 from the relation between r and phi above it does nt look like that could ever be less that zero unless C <0? Do i need to solve for C by the way?
YOur help is always, greatly appreciated!
Last edited: