Solving Related Rates Problem: Understanding Differentiation and the Power Rule

[fitz_calc]

Here is the solution to one of my problems:

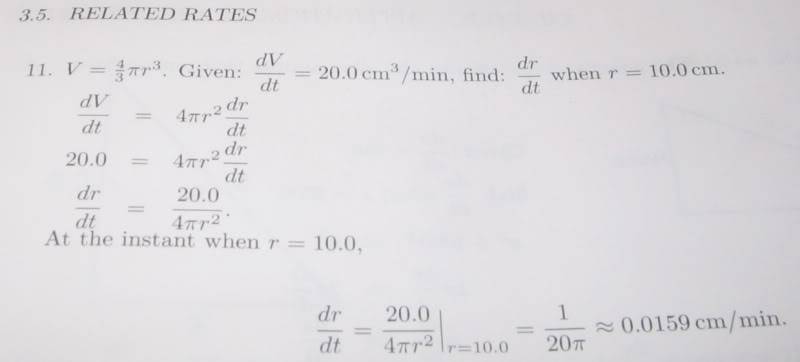
When inserting dV/dt to differentiate the equation as a function of time, why doesn't the book use the power rule on r^2 and multiply the entire equation by 2? I thought when dr/dt was put into the equation you had to differentiate?

 

[rocomath]

i don't see why there is a need to multiply by 2? if anything, dividing by 4 would clean things up.

and there is no need to apply the power rule on r^2 b/c it was already differentiated.

sorry i can't give you a more detailed answer.

 

[rock.freak667]

Why would they multiply by 2?

they differentiated it correctly.Unless you are differentiating the wrong statement.

\frac{d}{dt}(\frac{4}{3}\pi r^3)= (3(\frac{4}{3})\pi r^2))\frac{dr}{dt}

which is =4\pi r^2 \frac{dr}{dt}

 

[fitz_calc]

ahh yeah I was looking at the formula as being 4pi*r^2 instead of cubed, even though it was right in front of me in it's correct form!

Another question given this same example, why do you only differentiate r^2 -- why not 4 and pi as well?

 

[rocomath]

ahh yeah I was looking at the formula as being 4pi*r^2 instead of cubed, even though it was right in front of me in it's correct form!

Another question given this same example, why do you only differentiate r^2 -- why not 4 and pi as well?

r^3***

and we don't differentiate 4pi bc it's a constant

you could do the product rule on them but you would yield the same results

y=2x
y'=2