How Do I Find the Tension in a Cable at Different Angles?

[Saladsamurai]

I know this is an Engineering problem, but it's the Physics part of it I am having trouble with. The part I am stuck on is finding the TENSION in the cable from where theta=20 and then again where it equals 50.

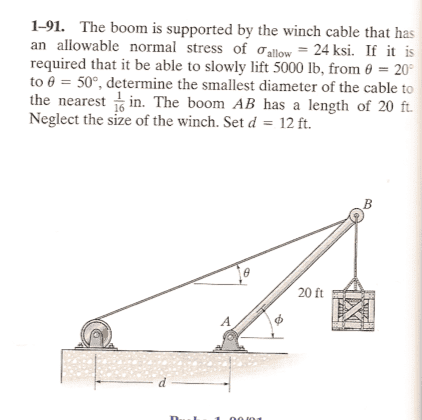
I have drawn a free-body, but I am having a really hard time finding out what I am doing wrong. I thought I could just use \sum F_y=0\Rightarrow -5000-T\sin50=0 which is blatantly incorrect! So I think I need to include the vertical reaction force at A which I can't seem to find

 

[PhanthomJay]

All forces , and all moments about about a point , must sum to zero when a system is in equilibrium.

 

[Saladsamurai]

Okay. I was thinking that too. So without phi and only theta, what point would you choose?

If I choose A it looks like I could use d*sin\theta for one moment and the reaction at Ay produces zero moment, but how would I find the moment arm to the force created by the weight of the crate if I don't know the angle the boom makes with the horizontal?

Thanks,
Casey

 

[Saladsamurai]

Okay. I was thinking that too. So without phi and only theta, what point would you choose?

If I choose A it looks like I could use d*sin\theta for one moment and the reaction at Ay produces zero moment, but how would I find the moment arm to the force created by the weight of the crate if I don't know the angle the boom makes with the horizontal?

Thanks,
Casey

Yeah, without \phi I don't see how to solve this problem?

 

[Pyrrhus]

With trigonometric you can find the values of phi for each of the theta cases.

 

[Saladsamurai]

I am so terrible at trig like this. I have no idea how to get the angle phi. I want to say I will probably need Law of Sines for this?

 

[Saladsamurai]

Alright, I got phi=32 when theta=20 by Law of Sines. If that's right I'd say I'm 90% there.

 

[Saladsamurai]

I would actually say that if taking the moments about C, then d is extraneous info. I don't need it.

It should be -20\cos32*5000+T\cos20=0\Rightarrow T=\frac{20\cos32*5000}{\cos20}=90.2kip for theta=20

This isn't working either. wtf. . . I suck at this.

 

[Pyrrhus]

I'm not understanding what you are doing. Did you take moment about A? where is C? and didn't you forget a lever arm?

 

[Saladsamurai]

There is no "C" in the problem. I am taking the Moment about A. The only forces acting on the Boom are weight of the crate and the tension in the cable and the reaction forces at A.

Taking moment about A the reactions go to zero. Taking counterclockwise as + I would have:

Scratch everything...I see I need 3 moment arms altogether. Let me get my sh@t together here...

 

[TVP45]

Casey,
I know you're new to statics and that sometimes makes it hard to see the question. Can you, by examination (just by looking at it), determine which angle is the worst case?

 

[andrevdh]

I cannot view your picture (my server blocks access to this site), but the reaction force of the arm of the boom (at the top) will be along the direction of the arm if the boom has a pivot at the bottom. This means that the resultant of the tension and the weight of the crate will be pointing down along the direction of the arm of the boom and will have the same magnitude as the reaction force of the boom.

 

[Saladsamurai]

Casey,
I know you're new to statics and that sometimes makes it hard to see the question. Can you, by examination (just by looking at it), determine which angle is the worst case?

I want to say that when theta=20 there would be more stress, I am not sure how to reason it out. . . I guess that if were to look at the extreme cases, that is ifthe boom were straight up, the cable would not have to do much to support it. . . where as when the boom starts to 'fall', the cable exerts more and more force since the weight of the crate is being directed away from the boom.

Sound right?

 

[TVP45]

So, if you assume you're right about that, can you solve the problem for that angle?

 

[Saladsamurai]

I can get the angle from Law of Sines and simple geometry. Then I should be able to find T by taking the moment about A.

The reactions at A produce zero moment, then I use the two components of T and their respective moment arms and the 5000 lb force and its respective moment arm and sum them all to zero.

I think that should do it? I tried it last night, but it did not work, however I was cooked from a long day and I think I kept making arithmetic errors.

But does my process sound right?