ehj
- 79
- 0
I'm currently working with lasers and in relation to that, fiber optics. In the book I'm reading there's a section regarding modes and their "group velocity". The text claims that there is the following relation:
v_g=v_p * sin(A)
where v_g is the group velocity and
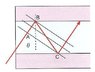
where v_p is the phase velocity and A is the incident angel as showed on the picture, although denoted as theta there.
From the picture you can see that the relation is reached by using trigonometry, and v_g is in this case simply the velocity in the direction along the fiber. My question is, if this is the general idea of group velocity? I thought group velocity was the velocity of the "amplitude wave" in a wave packet? Am I wrong, or are there just different meanings of group velocity?
v_g=v_p * sin(A)
where v_g is the group velocity and
where v_p is the phase velocity and A is the incident angel as showed on the picture, although denoted as theta there.
From the picture you can see that the relation is reached by using trigonometry, and v_g is in this case simply the velocity in the direction along the fiber. My question is, if this is the general idea of group velocity? I thought group velocity was the velocity of the "amplitude wave" in a wave packet? Am I wrong, or are there just different meanings of group velocity?