nyrychvantel
- 14
- 0
1.
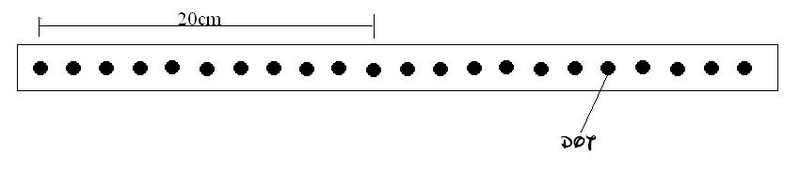
The diagram shows a strip of paper tape that has been pulled under a vibrating arm by an object moving at constant speed. The arm is vibrating regularly, making 50 dots per second.
What was the speed of the object?
A. 2.0cm/s B. 5.0cm/s C. 100cm/s D. 200cm/s
Completely clueless..
2. If you place 100cm³ of liquid water into freezer, will you get a 100cm³ ice cube?
The diagram shows a strip of paper tape that has been pulled under a vibrating arm by an object moving at constant speed. The arm is vibrating regularly, making 50 dots per second.
What was the speed of the object?
A. 2.0cm/s B. 5.0cm/s C. 100cm/s D. 200cm/s
Completely clueless..
2. If you place 100cm³ of liquid water into freezer, will you get a 100cm³ ice cube?