tjkubo
- 41
- 0
Homework Statement
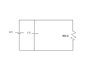
Find the current through each component of the circuit.
Homework Equations
Kirchhoff's laws
The Attempt at a Solution
I labeled the current through the left battery I1 and the current through the right battery I2. Therefore the current through the resistor is I1+I2. Using the voltage rule, I1+I2 = .01 A.
I have no idea how to find I1 and I2. Would current flow through both of them?