Solving for Tension & Angles in Ball Mass Problem: Help Needed!

AI Thread Summary
The discussion focuses on determining the tension and angles in a system involving two balls with different masses, where one ball has mass m and the other has mass 2m. The length of the thread connecting them is 2R, with R being the radius of the circle. The relationship between the angles is established using the equation m1*g*sinθ1 = m2*g*sinθ2, leading to the conclusion that sinθ1 = 2*sinθ2. By substituting θ2 with (2 - θ1) and solving the equations, the angles can be calculated. The problem emphasizes the need to account for the differing masses to accurately find the angles and tension in the system.
385sk117
Messages
50
Reaction score
0
http://ruliweb6.nate.com:8080/ruliboard/gup/img_link7/436/435945_1.jpg

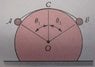
Ball A B
Mass m 2m

Length of tread is 2R where R is the radious of the Circle.
I have to find the tension on the tread and angles
I could have found the angles by assuming that the angle 1 and angle 2 are same
but as balls' masses are different, the angles must be different as well, and if they are different i don't think i can find the angle...
Any helps? Please TT
 

Attachments

  • 1.jpg
    1.jpg
    9.7 KB · Views: 448
Last edited by a moderator:
Physics news on Phys.org
Ball comes rest when
m1*g*sinθ1 = m2*g*sinθ2.
It is given that m2 = 2m1
So sinθ1 = 2*sinθ2...(1)
Length of the thread is 2R and radius is R.
So (θ1 + θ2) = 2R/R = 2 rad.
Put θ2 = (2 - θ1) in the eq.1 and solve for θ1.
 

Thread 'Struggling to understand the concept of this question (ice cube in water optics question)'

TL;DR Summary: I came across this question from a Sri Lankan A-level textbook. Question - An ice cube with a length of 10 cm is immersed in water at 0 °C. An observer observes the ice cube from the water, and it seems to be 7.75 cm long. If the refractive index of water is 4/3, find the height of the ice cube immersed in the water. I could not understand how the apparent height of the ice cube in the water depends on the height of the ice cube immersed in the water. Does anyone have an...
View full post »
Thread 'Variable mass system : water sprayed into a moving container'

Thread 'Variable mass system : water sprayed into a moving container'

Starting with the mass considerations #m(t)# is mass of water #M_{c}# mass of container and #M(t)# mass of total system $$M(t) = M_{C} + m(t)$$ $$\Rightarrow \frac{dM(t)}{dt} = \frac{dm(t)}{dt}$$ $$P_i = Mv + u \, dm$$ $$P_f = (M + dm)(v + dv)$$ $$\Delta P = M \, dv + (v - u) \, dm$$ $$F = \frac{dP}{dt} = M \frac{dv}{dt} + (v - u) \frac{dm}{dt}$$ $$F = u \frac{dm}{dt} = \rho A u^2$$ from conservation of momentum , the cannon recoils with the same force which it applies. $$\quad \frac{dm}{dt}...
View full post »

Similar threads

Tension in a deformed cylindrical bag on a surface
Replies
18
Views
1K
Resolving forces: Mass on a string
Replies
4
Views
4K
Finding Charge & Tension of a Suspended Cork Ball
Replies
3
Views
4K
What is the formula for tension at various angles in a constrained mass system?
Replies
5
Views
2K
System of two pulleys and three masses
Replies
22
Views
6K
Tension of wire attached to 45-kg ball.
Replies
2
Views
8K
Problem involving space elevators
Replies
19
Views
2K
Hanging pith balls on a thread...charge, Fg, Fe and tension
Replies
2
Views
3K
Solving Tetherball Problem: Find Tension & Angle θ
Replies
5
Views
4K
Circular wire with ball and spring problem
Replies
6
Views
2K

Hot Threads

Recent Insights

Back
Top