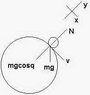
OK, a bit to sort out here:
1. Weight:
This is equal to mg, acting downwards.
However, it's "downwards" is not always the convenient direction to think weight in terms with!
For example, on a slope, the two most convenient directions are a)tangential to the slope, b)normal to the slope.
But, "downwards" is rarely coincident with either of these directions in space; rather, "downwards" must be seen as having components in both directions; a normal component, and a tangential component.
To be specific, let a sloping plane make angle \theta to the horizontal (normal to "downwards")
We use \vec{i} to be a unit vector in the horizontal direction, wheres \vec{j} is a unit vector in the "upwards" direction.
Also, let \vec{t} be a unit vector in the tangential direction to the sloping plane, while \vec{n} is a unit vector in the normal direction of the sloping plane ("normal" meaning in a direction at right angles to the plane)
We have the following relation for the tangent vector:
\vec{t}=\cos\theta\vec{i}+\sin\theta\vec{j}
Since \vec{n} is normal to the tangent, we may write:
\vec{n}=-\sin\theta\vec{i}+\cos\theta\vec{j}
We now proceed to invert these relations, that is, express \vec{i},\vec{j} in terms of \vec{t},\vec{n}
By the choices we've made, we get:
\vec{i}=\cos\theta\vec{t}-\sin\theta\vec{n}
\vec{j}=\sin\theta\vec{t}+\cos\theta\vec{n}
The weight of an object of mass m, \vec{W} is in the downwards direction, so clearly we have:
\vec{W}=-mg\vec{j}
Hence, expressed in terms of vectors \vec{t},\vec{n} the weight
has the form (substituting for \vec{j}):
\vec{W}=-mg\sin\theta\vec{t}-mg\cos\theta\vec{n}
It is crucial that you understand this, so I'll stop here at the moment.
Please post any questions you might have.