NickyuTse
- 9
- 0
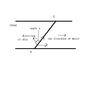
in order to find out the speed of a new steamship,a scientist comes up with a idea to slove it e makes the steamship sail from A to B and then return to A from B(look at the image). only when the angle between the line AB and the direction of the sreamship is a,the streamship can sail though the line AB,and the time it takes is t1. and the time of coming back though BA is t2. the distance of AB is S. question:what is the speed of the new streamship?
e makes the steamship sail from A to B and then return to A from B(look at the image). only when the angle between the line AB and the direction of the sreamship is a,the streamship can sail though the line AB,and the time it takes is t1. and the time of coming back though BA is t2. the distance of AB is S. question:what is the speed of the new streamship?
 e makes the steamship sail from A to B and then return to A from B(look at the image). only when the angle between the line AB and the direction of the sreamship is a,the streamship can sail though the line AB,and the time it takes is t1. and the time of coming back though BA is t2. the distance of AB is S. question:what is the speed of the new streamship?
e makes the steamship sail from A to B and then return to A from B(look at the image). only when the angle between the line AB and the direction of the sreamship is a,the streamship can sail though the line AB,and the time it takes is t1. and the time of coming back though BA is t2. the distance of AB is S. question:what is the speed of the new streamship?