Bernoulli's principle with venturi effect

[Diokaef]

So, I need some info on how to get the data that I'm missing on my project.

My english is not great and is very hard for me to try figure this out by myself so if you guys could help me out I will appreciate.

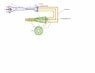
I need to know how much vacuum in HG I will get at the B on my picture, and if will increase the suction from my B inlet (500 CFM at 700F) mean increase its velocity output from 500CFM to ?

I will be using fans to provide a 75mph wind at the A inlet then reduce the pipes until I can divide that to 12 hoses with inside of 1/8" 36" long to a collector kind thing then will flow around of a 2 1/4" pipe, on this pipe I have already a 500CFM at 700F and I need to know how much if any increase would have at that stage (ex. 500 CFM increase to 700 CFM)

Man, I'm really having problems with this thing.

 

[rcgldr]

Mass flow across any cross section in this device will be constant. CFM will only increase if the temperature increases enough or pressure decreases enough to create a significantly large decrease in density.

Assuming this is a real device, then pressure will decrease even in the constant diameter section of pipes, due to friction with the walls of the pipes, and viscosity (friction within the gas itself).