amrbekhit
- 11
- 1
A linear actuator is wedged between two solid walls as shown in the diagram below. The linear actuator is pushing outwards with a force of 10N. What are the magnitudes of the forces labelled in the diagrams?
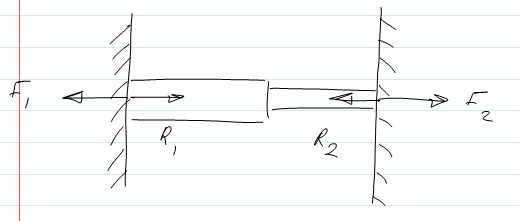
I reckon that F1 = F2 = R1 = R2. However, I'm not sure if F1 = F2 = 5N or 10N. I'm guessing 10N.
Any thoughts?
--Amr
I reckon that F1 = F2 = R1 = R2. However, I'm not sure if F1 = F2 = 5N or 10N. I'm guessing 10N.
Any thoughts?
--Amr