Four_FUN
- 2
- 0
Homework Statement
Consider a two stage compressor. The working fluid is air. The first stage compressor takes the air at P_1 and T_1. It compresses the air to the pressure P_2. Between the two compressors, the air is cooled at constant pressure from T_2 to T_1 (I believe this is the other way around but this is how its written). It is then compressed by the second compressor to the pressure P_3
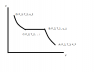
a) draw the process in P-v coordinates
b) Determine the work per unit mass to run the compressor, as a function of P_1, P_2, P_3, T_1, gamma and c_p (specific heat at constant pressure).
c) Determine the pressure, P_2, which minimizes the compressor work.
Homework Equations
Delta(U) = Q - W (heat to system - work by system) (1)
PV=mRT, where R=287 kg/(mol K) and m = 1kg (2)
du = c_v*dT (3)
dh = (dq when P is constant) = c_p*dT (4)
The Attempt at a Solution
My P-v diagram is as shown in the (crude) paint drawing
Now to find the work I use the definition of pressure-volume work along the paths A-B and C-D to obtain:
W_AB = R*T_1*LN(p_1/p_2)
W_CD = R*T_2*LN(p_2/p_3)
using specific heats and applying (3) and (4) to (1)
W_BC = (T_2 - T_1)*(c_p - c_v) = R*(T_2 -T_1)
Now I imagine that the answer is the sum of the above. Unfortunatelly though I have been unable to get rid of that T_2 and presumably in the process get gamma to appear somewhere. If I could achieve that I would simply calculate dW/dp_2 == 0 and hopefully get an answer. I would like some help in getting rid of T_2 and any hints or comments on my work thus far.