Vertical Latch Friction Problem

Houdini176

1. The problem statement, all variables and given/known data

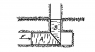
"A side view of a simplified form of vertical latch is as shown. The lower member A can be pushed forward in its horizontal channel. The sides of the channels are smooth, but at the interfaces of A and B, which are at 45 degrees with the horizontal, there exists a static coefficient of friction U. What is the minimum force F that must be applied horizontally to A to start motion of the latch, if B has a mass m?"

I always found an incorrect "solution" to this, help finding the correct method would be appreciated.

2. Relevant equations

F*d=mg*d

-mg-U*N*sin(45)+F=0

N*cos(45)=F

3. The attempt at a solution

The block B should experience three forces in the vertical direction: the vertical component of the friction between the two blocks, the vertical component of the normal force, and gravity. The crux of the problem seems to be finding the normal force.

If there was no friction and the blocks were moving quasi-statically, B would move vertically as far as A moved horizontally. Using the conservation of energy, F*d=mg*d, and F=mg. Using this, it seems reasonable to say that the vertical component of the normal force is equal to the force placed on the block A. Because F is the vertical component of the normal force, it follows that:

F/cos(45)=N

(I'm really not sure how else to find the normal force, and I suspect that this step is where I've gone wrong.)

Because the question asks to find the minimum force needed to make the arrangement move, all the forces on B should add to 0.

-mg-U*N*sin(45)+F=0

-mg-U*F*sin(45)/cos(45)+F=0
-mg-U*F+F=0
(1-U)F=mg
F=mg/(1-U)

Unfortunately, the answer given is F=(1+U)mg/(1-U).

If I go backwards from that answer, it suggests that the vertical component of the normal force is (F+mg), which I refuse to believe. After all, if I applied a force equal to mg to the block, the vertical component of the normal force wouldn't be 2mg.

Anyway, any help would be greatly appreciated, along with any problem solving advice in general. I've been trying to teach myself physics, and I usually can't correctly solve the problems. I usually feel that my reasoning is sound, but it turns out not to be. It's disheartening.

Attached Thumbnails

 

Houdini176

Solved. In case anyone is curious, the conservation of energy relation I used is incorrect. The conservation of energy is that simple if there is no friction, but in the case of this problem there is friction. Therefore, the work done by the force applied to block A gets divided into increasing the potential energy of B AND moving against friction.

The solution is to consider the static equilibrium of both blocks. Since the net force on each block will include the normal force, you can easily find the sum of every force on each individual block, set that sum to 0, solve for N, and substitute N out of the equations. You'll have a solution for F.