Illgresi
- 9
- 0
Here goes try number two, the forum deleted my last post. 
First time poster, so hopefully I'm following the rules, I do apologise if I'm not. I have a problem with my lab report, I would be very grateful if anyone could help. Thanks.
I'm writing a tensile test lab report and have hit a snag along the way. We were given three unknown specimens and through analysis of the recorded data, are to make educated guesses as to what they are. I have all but confirmed the first two are high carbon steel and aluminium of some description. Young's modulus, UTS and 0.2% proof stress are all accurate. In the case of the third sample, my modulus is far below what I would expect (22.5 GPa). I am however, convinced it is cast iron due to a number of factors; the shape of the load/extension diagram, the uts/fracture stress and above all the fact that it smelled like cast iron.
σ=F/A, ε=ΔL/L0, E=σ/ε
My successful attempt at calculating the modulus for samples A and B was to take an average (mean) across the entire elastic region for both stress and strain, and using these values to calculate. Essentially creating a best fit line, which made sense given E is actually the gradient. It worked superbly for the first two samples; 206.6 GPa for the steel sample, and 68 GPa for the Aluminium.
The problem with the 'Cast Iron' sample, is that it doesn't have any apparent linear portion; it curves from the origin to the fracture point. I was hoping someone could provide some ideas what to do. Perhaps there is a special technique for materials of this type?
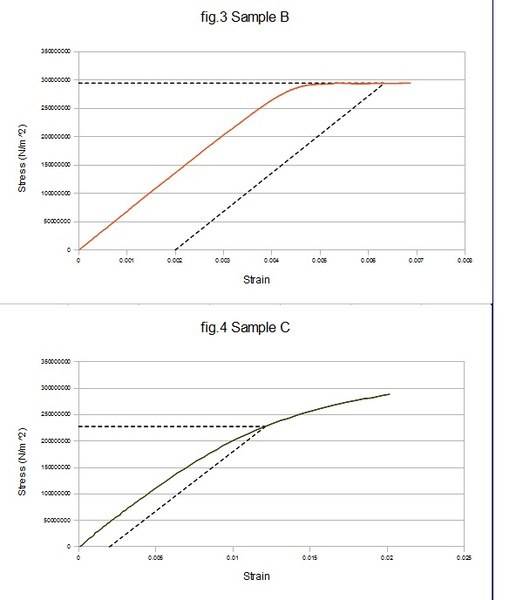
I have included a picture of the stress/strain diagram of sample B (Al) and Sample C ('cast iron') to illustrate what I mean.
FYI, the dotted lines represent 0.2% offset, as you can see, it is particularly accurate for Sample B.
Many, many thanks for any help.

First time poster, so hopefully I'm following the rules, I do apologise if I'm not. I have a problem with my lab report, I would be very grateful if anyone could help. Thanks.
Homework Statement
I'm writing a tensile test lab report and have hit a snag along the way. We were given three unknown specimens and through analysis of the recorded data, are to make educated guesses as to what they are. I have all but confirmed the first two are high carbon steel and aluminium of some description. Young's modulus, UTS and 0.2% proof stress are all accurate. In the case of the third sample, my modulus is far below what I would expect (22.5 GPa). I am however, convinced it is cast iron due to a number of factors; the shape of the load/extension diagram, the uts/fracture stress and above all the fact that it smelled like cast iron.
Homework Equations
σ=F/A, ε=ΔL/L0, E=σ/ε
The Attempt at a Solution
My successful attempt at calculating the modulus for samples A and B was to take an average (mean) across the entire elastic region for both stress and strain, and using these values to calculate. Essentially creating a best fit line, which made sense given E is actually the gradient. It worked superbly for the first two samples; 206.6 GPa for the steel sample, and 68 GPa for the Aluminium.
The problem with the 'Cast Iron' sample, is that it doesn't have any apparent linear portion; it curves from the origin to the fracture point. I was hoping someone could provide some ideas what to do. Perhaps there is a special technique for materials of this type?
I have included a picture of the stress/strain diagram of sample B (Al) and Sample C ('cast iron') to illustrate what I mean.
FYI, the dotted lines represent 0.2% offset, as you can see, it is particularly accurate for Sample B.
Many, many thanks for any help.