How to Determine the Brightness of Bulbs in a New Configuration?

  • Thread starter Thread starter hms.tech
  • Start date Start date
  • Tags Tags
    Bulb Power
AI Thread Summary
To determine the brightness of bulbs in a new configuration, the relationship between power and voltage is crucial, as brightness is proportional to power. The equations P = V²/R and P = I²R can yield different results depending on the approach used. In this case, bulb "g" receives 2V, making it brighter than normal, while bulb "h" remains at normal brightness with voltage V. Clarification is sought on whether it is acceptable to rely solely on one formula for accurate results. Posting detailed calculations is recommended for verification of the findings.
hms.tech
Messages
246
Reaction score
0

Homework Statement



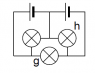
See attachment
The question asks to calculate the brightness of the bulbs(g and h) in this new configuration.


Homework Equations



Since brightness \propto Power

P= V^{2}/R
P= I^{2}R
E.M.F of One cell : V

The Attempt at a Solution



I used the equation P = V^(2)/R

Since the Voltage across "g" will be 2V and its Resistance is exactly the same as in the reference Attachment, "g" will be brighter than normal.
Similarly, since the Voltage across "h" is going to be V, "h" must be of normal brightness.

I am not sure if my answers make sense since if we apply the 2nd formula : P=R*I^2
we would get a different set of results .

Is it O.K to just rely on one of the two formulas and deduce the final answer based on say P=V^(2)/R ? Would the answers be authentic ?
 

Attachments

  • Capture.PNG
    Capture.PNG
    7.8 KB · Views: 454
  • Capture5.PNG
    Capture5.PNG
    2.6 KB · Views: 438
Physics news on Phys.org
hms.tech said:
I am not sure if my answers make sense since if we apply the 2nd formula : P=R*I^2
we would get a different set of results .
Not if you do it correctly. Pls post your working.
 
Thread 'Variable mass system : water sprayed into a moving container'

Thread 'Variable mass system : water sprayed into a moving container'

Starting with the mass considerations #m(t)# is mass of water #M_{c}# mass of container and #M(t)# mass of total system $$M(t) = M_{C} + m(t)$$ $$\Rightarrow \frac{dM(t)}{dt} = \frac{dm(t)}{dt}$$ $$P_i = Mv + u \, dm$$ $$P_f = (M + dm)(v + dv)$$ $$\Delta P = M \, dv + (v - u) \, dm$$ $$F = \frac{dP}{dt} = M \frac{dv}{dt} + (v - u) \frac{dm}{dt}$$ $$F = u \frac{dm}{dt} = \rho A u^2$$ from conservation of momentum , the cannon recoils with the same force which it applies. $$\quad \frac{dm}{dt}...
View full post »

Similar threads

Determining the Change in Bulb Brightness by Changing Circuit
Replies
6
Views
1K
Differences in the Brightness of bulbs for 2 separate circuits
Replies
1
Views
2K
Which of the bulbs glow brightest and least bright?
Replies
8
Views
2K
Current, voltage : brightness of bulb in parallel or series
Replies
2
Views
4K
Brightness of bulbs depending on their watt level
Replies
11
Views
2K
Comparing the brightness of each bulb in a circuit
Replies
6
Views
2K
How to find the power consumed by the light bulb
Replies
19
Views
3K
Which bulb will glow brighter in a series and parallel circuit?
Replies
5
Views
2K
Transformer and the brightness of bulbs
Replies
11
Views
2K
Inductor and bulb in an circuit
Replies
7
Views
2K

Hot Threads

Recent Insights

Back
Top