voko said:
Assume for a second there is no tractive resistance. Would the train be able to go up the gradient indefinitely?
The train will go further if there was no tractive resistance, however, it wouldn't go on forever due to gravity?
SteamKing said:
Acceleration is not just the difference in velocity. Remember, the units of acceleration are m/s^2.
Think about the problem for a minute before worrying about what formulas to use. The train is merrily going on its way at constant velocity. When the train encounters the hill, the engineer closes the throttle and let's the train coast up the hill. When going up the hill, why does the train's velocity drop? Is it just because of the resistance to motion? Or is it also because when traveling up the hill, the train is being raised to a higher elevation?
It is because it is traveling to a higher elevation, gravity comes into play?
My lecturer hinted that its the height distance I calculate, then use trigonometry to calculate the distance traveled up the gradient of 8degrees.
CWatters said:
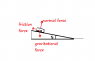
How about drawing a diagram showing the forces acting on the train when it's on the slope?
I have now drawn one, I'm not sure quite sure if this is correct but below is my attempt,
The train is moving at a force of, F = 80000 x 19.4 = 1552000N
The tractive resistance force is F = 80000 x 0.07 = 5600N
so we subtract tractive resistance force from moving force
1552000-5600 = 1546400N
Our acceleration now (or rather deceleration) with tractive resistance implemented is
1546400N/80000 = 19.33m/s
Then v^2 = u^2 + 2a x d
so d = -u^2 / 2a
distance = -19.33^2 / (2 x 9.81) = 19m (vertical distance?)
Using trigonometry,
Distance (on the gradient) = 19m/sin(8) = 136.5m
That sounds a reasonable distance to me?
If the above is correct, my next step is to
"Prove my answer by an alternative method, compare and contrast the 2 methods."
1 Method to be used is conservation of energy (as used) and the other is D'Alembert's principle which I have never done, I have just went through a powerpoint explaining the D'alemberts principle but it was far to complex for me. Is there a simplified explanation or could someone summarize the principle for me.
All I gathered from it that it is used when there are multiple forces on a mass, which can be used where an object can move in xyz.