Relativistic velocity addition

[DiracPool]

I feel I understand relativistic velocity addition fairly well. However, the way I usually see it modeled is with two travelers moving in the same direction. Bob is in a spaceship traveling at 0.6c and shines his flashlight in the direction of travel. An inertial observer, Alice, relative to the spaceship will not see the leading edge of the flashlight beam travel at 1.6c relative to herself, she will see a speed somewhat less than c once the two velocities are plugged into the relativistic velocity addition formula.

I've got that, but let's take another scenario. Let's say Charlie is now the internal observer, and we place Alice 10 light minutes to Charlies left, and Bob 10 light minutes to Charlies right. Each are stationary relative to one another and in the same proper time frame. Now we have both Bob and Alice shine a flashlight at each other, with Charlie hanging out in the center equidistant from the two. What I am visualizing is Charlie seeing Alice's light beam traveling to the right toward Bob at c, and Bob's light beam traveling to left toward Alice at c.

Sounds ok so far, but what about when the leading edge of the beams approach each other? Won't Charlie see these as traveling at 2c relative to each other? Or, to put it another way, won't the distance or displacement between the two leading edges of the beams be shrinking at a rate of 2c? Is this type of thing allowed? Or does the relativistic velocity addition formula have a way to handle this situation too?

 

[DiracPool]

Update:

Coincidentally, I just read Jtbells post in this thread:https://www.physicsforums.com/showthread.php?t=765085

The separation speed of the two bullets, as measured by you in your reference frame, is c. That is, the distance between the two bullets increases at the rate c in your reference frame.

The relative speed of the two bullets is 0.8c, as per the "relativistic velocity addition" formula. This is the speed of one bullet in the reference frame in which the other one is stationary, i.e. the speed of one bullet as "observed" by the other one.

Does this apply to my scenario? That is, the two beams have a separation speed (or converging speed in my example) of 2c? Whereas they would have a relative speed of c? We can use the two bullet model, each traveling at say .9c to get around the "stationary" light issue in the relative speed version if that's an issue?

 

[stevendaryl]

Sounds ok so far, but what about when the leading edge of the beams approach each other? Won't Charlie see these as traveling at 2c relative to each other? Or, to put it another way, won't the distance or displacement between the two leading edges of the beams be shrinking at a rate of 2c? Is this type of thing allowed? Or does the relativistic velocity addition formula have a way to handle this situation too?

There are two different notions of "relative velocity": Velocity relative to an inertial frame, and "closing velocity" between two different objects, as measured in an inertial frame.

The velocity addition formula is applicable in one very special case:

• Let $F_1$ be an inertial frame.
• Let $F_2$ be a second inertial frame such that an object at rest in frame $F_2$ is moving at speed $v$ as measured in frame $F_1$ (in the x-direction, say).
• Let there be an object that is moving at speed $w$ relative to frame $F_2$ (again, in the x-direction, say).
• Then relative to frame $F_1$, the object is moving at speed $w' = \dfrac{v+w}{1+\frac{vw}{c^2}}$

So the velocity addition formula is about how velocities transform between two different frames. That's not relevant to the situation where there are two different light beams both moving toward Charlie from opposite directions. In that situation, you aren't transforming between two different frames, you're just computing the rate at which the distance between the two light beams decreases. The answer to that is exactly what you would think: it's just the sum (or difference) of the two velocities. So for the two beams, the rate that they are approaching each other, as measured by Charlie, is 2c.

 

[DiracPool]

Great, thanks stevendaryl, that was just what I was looking for.

 

[ghwellsjr]

I feel I understand relativistic velocity addition fairly well. However, the way I usually see it modeled is with two travelers moving in the same direction. Bob is in a spaceship traveling at 0.6c and shines his flashlight in the direction of travel. An inertial observer, Alice, relative to the spaceship will not see the leading edge of the flashlight beam travel at 1.6c relative to herself, she will see a speed somewhat less than c once the two velocities are plugged into the relativistic velocity addition formula.

You just said "two travelers moving in the same direction" and then you described only one, Bob, moving. Are we to assume that Bob is moving in Alice's rest frame or did you mean that both of them are moving according to some other frame?

In any case, neither Bob nor Alice can see the flash of light that is emitted by Bob, unless, of course, Alice is in front of Bob and he shines the light on her, but since you didn't say, what are we to assume?

What you should understand is that according to the precepts of Special Relativity, light propagates at c according to any inertial frame in any direction you want to consider. It's not something that observers can see. So it is not correct to say that Alice "will see a speed somewhat less than c", first because she cannot see light's speed no matter what it might be and second because in her inertial rest frame the light is defined to travel at exactly c, not somewhat less or somewhat more, just c.

You would do well to understand the Lorentz Transformation process which is very simple in the inline inertial cases that you present here. You could start with Bob in his rest frame emitting a flash of light at c and then transform to a frame in which he is traveling at 0.6c and you would see that the light is still traveling at c whether or not Alice is at rest or traveling or even present in this new frame.

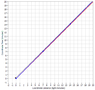
Here, let me show you. This is a simple spacetime diagram showing Bob as the thick blue line with dots indicating 1-minute ticks of his clock:

He emits a flash of light at time zero towards a reflector depicted in red that is 5 light minutes away. He cannot see this flash of light nor can he see or measure or have any indication of its speed as it is traveling away from him. The reflection eventually shows up back at his location at his time of ten minutes and so he measures that the time it took for the light to make the round trip to the reflector and back as ten minutes. But for all he knows it could have taken 80% of that time to get to the reflector and 20% of that time to get back. However, according to Special Relativity, we assert without any specific physical proof or evidence that the light spent 50% of the time getting to the reflector and the other 50% of the time getting back.

Now we can transform to a frame in which Bob is traveling at 0.6c:

Note that in this frame the light does take 80% of the time to get to the reflector and 20% of the time to get back but the light is still traveling at c. So why did you say that the light would be traveling at somewhat less than c? Did you actually do the calculation?

I've got that, but let's take another scenario. Let's say Charlie is now the internal observer, and we place Alice 10 light minutes to Charlies left, and Bob 10 light minutes to Charlies right. Each are stationary relative to one another and in the same proper time frame. Now we have both Bob and Alice shine a flashlight at each other, with Charlie hanging out in the center equidistant from the two. What I am visualizing is Charlie seeing Alice's light beam traveling to the right toward Bob at c, and Bob's light beam traveling to left toward Alice at c.

Again, Charlie won't be able to see Alice's beam until it hits him and he won't be able to see Bob's beam until it hits him from the other side. If Charlie sees both beams hit him at the same time, then according to the precepts of Special Relativity, Alice and Bob emitted them at the same time according to their mutual rest frame. That's the definition of simultaneity as shown in this spacetime diagram:

But when Charlie sees both beams, he has no way of measuring what speed they approached him at. The best he can do is start a pair of timers when the beams pass by him and allow the two beams to reflect off a pair of reflectors some equal distance away on either side of him and wait for the reflections to get back to him. Then he can calculate what the round trip speed of the two beams is based on the distance to the reflectors. Finally, he makes the assumption that the beams traveled away from him to the reflectors in the same amount of time that it took for the reflections to travel back to him and that allows him to implement the definition of the one-way speed of light according to Special Relativity.

Sounds ok so far, but what about when the leading edge of the beams approach each other? Won't Charlie see these as traveling at 2c relative to each other? Or, to put it another way, won't the distance or displacement between the two leading edges of the beams be shrinking at a rate of 2c? Is this type of thing allowed? Or does the relativistic velocity addition formula have a way to handle this situation too?

When you ask about the speed of one beam relative to the other beam, you are trying to establish a rest frame for light which is not possible so there is no answer to your question. But the other way of asking the question is allowed as long as you understand that it's not something that Charlie can measure but rather it is simply the definition of how light propagates in an inertial reference frame.

 

[ghwellsjr]

Update:

Coincidentally, I just read Jtbells post in this thread:https://www.physicsforums.com/showthread.php?t=765085

The separation speed of the two bullets, as measured by you in your reference frame, is c. That is, the distance between the two bullets increases at the rate c in your reference frame.

The relative speed of the two bullets is 0.8c, as per the "relativistic velocity addition" formula. This is the speed of one bullet in the reference frame in which the other one is stationary, i.e. the speed of one bullet as "observed" by the other one.

Does this apply to my scenario? That is, the two beams have a separation speed (or converging speed in my example) of 2c? Whereas they would have a relative speed of c? We can use the two bullet model, each traveling at say .9c to get around the "stationary" light issue in the relative speed version if that's an issue?

Bullets are different from photons but you can stipulate that the bullets are going as close to the speed of light as you desire to see that the speed of one bullet approaches c in the rest frame of the other bullet and vice versa. But you cannot use that scheme as a way to circumvent the fact that you cannot do the same thing with photons. You can have one photon going at c in one direction and one bullet going at just under c in the opposite direction and calculate by the formula that the speed of the photon in the rest frame of the bullet is c. How could it be otherwise? Remember, photons travel at c in all inertial reference frames by definition.

You can also talk about the closing or separation speed between two objects (either bullets or photons) but that is not the speed of anything, it's just an algebraic calculation.

Now I'd like to show you some more spacetime diagrams to hopefully help you understand better what is going on. First, let's start with the two bullet model where they are each traveling away from you (blue) at 0.9c in opposite directions. I'm only going to show the one going to the left (black) for a short distance in order to keep the diagram manageable but the other one going to the right (red) will be shown going a much larger distance:

What I'm showing in the above diagram is how the red bullet can measure the speed of the black bullet. In order to do this, it has to determine the distance to the bullet at two different times. It already knows it a the beginning, it's zero at time zero. In order to determine a second distance at a later time, it has to send a light (or radar) signal to the black bullet and then wait for the reflection (or return echo) to get back to the red bullet. Meanwhile, the red bullet keeps track of when it sent the signal (according to its own clock marked off by the dots indicating 1-minute intervals) and when the reflection is received. In the above example, it looks like the red bullet sent the signal at its time of 0.05 minutes (look at the very bottom of the diagram) and the reflection was received at 19 minutes. It then takes one half of the difference between those two times (9.475 minutes) and assumes that to be a measure of the distance away (9.475 light minutes) that separated the two bullets at some particular time. That particular time is the average of those two times (9.525 minutes). Since the first separation was zero at time zero, all we have to do is divide the determined separation by the determined time to get the speed. That comes out to be 9.475/9.525 = 0.9948c. (The answer from the formula is 0.9945c.)

Next let's transform to the red bullet's rest frame:

In the red bullet's rest frame, we can see that the same observations and calculations are made by the red bullet, and the diagram shows those results explicitly.

Now let's see what happens when we use a photon going to the left and a bullet going to the right. We have to make a slight change as noted in my first post since the red bullet cannot determine the location of the photon by sending another signal after it, which could never catch up. Instead, we have to bounce a reflection off of some object in the path of the photon and get it to reflect back to the red bullet. It doesn't matter when or where we do this, just as long as the photon reflects back from something. So I've put in a reflection event at -2 light minutes and at 2 minutes according to blue's rest frame:

Now when the red bullet does the same calculations that it did before with the black bullet, it uses the start time of zero and the return time of 17.4 minutes. This results in a separation distance of 8.7 light minutes at a time of 8.7 minutes which when divided yields a speed of 1c. (The formula also yields 1 as you should have figured out by now.)

Transforming to the rest frame of the red bullet, we see this result confirmed:

Now what if we tried to transform to the rest frame of the photon? Well, we know that we cannot do that but let's at least transform to -0.9c and see how close we get:

Well, we can see that even though the reflection event moves closer to the origin, it still is sticking out there at a 45-degree angle from the origin and showing no inclination to arrive at the x=0 axis which would be necessary to achieve the rest frame of the photon.

Let's transform even closer, to -0.99c:

Still no luck. No matter how close we transform to c, that reflection event will always be at a 45-degree angle from the origin. We just can't get it on the x=0 axis.

 

[DiracPool]

You just said "two travelers moving in the same direction" and then you described only one, Bob, moving. Are we to assume that Bob is moving in Alice's rest frame or did you mean that both of them are moving according to some other frame?

Good catch. I meant Bob was moving in Alice's rest frame. The two "travelers" are Bob and the rocket ship. I should have been more clear. In any case, thank you for the diagrams and in-depth explanation.