Lagrange Definition and 510 Threads
-
A
Lagrange Multipliers to find max/min values
Homework Statement Use Lagrange multipliers to find the max and min values of the function subject to the given constraints: f(x,y,z)= x2y2z2 constraint: x2 + y2 + z2 = 1 Homework Equations ∇f = ∇g * λ fx = gx * λ fy = gy * λ fz = gz * λ The Attempt at a Solution i can't solve...- arl146
- Thread
- Lagrange Lagrange multipliers
- Replies: 9
- Forum: Calculus and Beyond Homework Help
-
A
Lagrange Multipliers to find max/min values
Homework Statement Use Lagange Multipliers to find the max and min values of the function subject to the given constraint(s). f(x,y)=exp(xy) ; constraint: x^3 + y^3 = 16 Homework Equations \nablaf = \nablag * \lambda fx = gx * \lambda fy = gy * \lambda The Attempt at a Solution...- arl146
- Thread
- Lagrange Lagrange multipliers
- Replies: 7
- Forum: Calculus and Beyond Homework Help
-
G
Lagrange Multipliers: Minimum and Maximum Values
Homework Statement I am trying to find the min and max values of f(x,y)=2x^2 + 3y^2 subject to xy=5. Homework Equations f(x,y)=2x^2 + 3y^2 subject to xy=5 \mathbf\nablaf=(4x, 6y) \mathbf\nablag=(y,x) The Attempt at a Solution When I go through the calculations, I end up with two critical...- goblan
- Thread
- Lagrange Lagrange multipliers Maximum Minimum
- Replies: 6
- Forum: Calculus and Beyond Homework Help
-
X
Max/Min of f(x,y,z) with Lagrange Multipliers
Homework Statement Use Lagrange multipliers to ¯nd the maximum and mini- mum value(s), if they exist, of f(x; y; z) = x^2 -2y + 2z^2 subject to the constraint x^2+y^2+z^2 Homework Equations The Attempt at a Solution Basically after I find the gradient of the functions I get this. 2x=2x lamda...- xdrgnh
- Thread
- Lagrange Lagrange multipliers
- Replies: 3
- Forum: Calculus and Beyond Homework Help
-
P
Max/Min of f(x,y)=x^2+6y Using Lagrange Multipliers
Use lagrange multipliers to find max/min of f(x,y)=x^2+6y subject to x^2-y^2=5 grad f =λgrad g 2x=2xλ, λ=1 6=-2yλ, λ=-3/y 1=-3/y, y=-3 x^2-(-3)^2=x^2-9=5 x^2=14 x=+/-√14 two points are √14, -3 and -√14, -3 plugging both points into f(x,y) gives me the same answer. now what?- Pi Face
- Thread
- Lagrange
- Replies: 2
- Forum: Calculus and Beyond Homework Help
-
X
Lagrange Polynomial Interpolation
Homework Statement Find the polynomial p(x) of degree 20 satisfying: p(-10) =p(-9) = p(-8) = ...=p(-1) = 0 p(0) = 1 p(1) = p(2) = p(3) = ...p(10) = 0 Homework Equations L(x) := \sum_{j=0}^{k} y_j \ell_j(x) The Attempt at a Solution i tried using the formula above: a =...- xkellyy
- Thread
- Interpolation Lagrange Polynomial
- Replies: 5
- Forum: Calculus and Beyond Homework Help
-
I
Graduate Lagrange multipliers with vectors and matrices
My textbook is using Lagrange multipliers in a way I'm not familiar with. F(w,λ)=wCwT-λ(wuT-1) Why is the first order necessary condition?: 2wC-λu=0 Is it because: \nablaF=2wC-λu Why does \nablaF equal this? Many thanks! Edit: C is a covariance matrix- IniquiTrance
- Thread
- Lagrange Lagrange multipliers Matrices Vectors
- Replies: 1
- Forum: Linear and Abstract Algebra
-
G
Solving Lagrange Charpit Homework Equation
Homework Statement Use Charpits equations to solve 4u\frac{\partial u}{\partial x} = (\frac{\partial u}{\partial x})^2 where u=1 on the line x+2y=2 Homework Equations The Attempt at a Solution from the charpit equations i get \frac{dx}{dt} = 4u \frac{dy}{dt} = -1...- gtfitzpatrick
- Thread
- Lagrange
- Replies: 1
- Forum: Calculus and Beyond Homework Help
-
F
Lagrange Multiplier theory question
Homework Statement I made this up, so I am not even sure if there is a solution Let's say I have to find values for which these two inequality hold x^2 + y^5 + z = 6 and 8xy + z^9 \sin(x) + 2yx \leq 200And by Lagrange Multipliers that \nabla f = \mu \nabla g So can I let f = 8xy + z^9 \sin(x)...- flyingpig
- Thread
- Lagrange Lagrange multiplier Theory
- Replies: 3
- Forum: Calculus and Beyond Homework Help
-

Graduate Applying Lagrange Multipliers to Optimization with Binary Variables
Dear all, I have an optimization problem with boundary conditions, the type that is usually solved with Lagrange multipliers. But the (many) variables my function depends on can take only the values 0 and 1. Does anyone know how to apply Lagrange multipliers in this case? I am a...- Angelos K
- Thread
- Lagrange Lagrange multipliers
- Replies: 1
- Forum: General Math
-
D
Graduate Showing that the euler lagrange equations are coordinate independent
so i know for example that d/dt (∂L/∂x*i) = ∂L/∂xi for cartesian coordinates, where xi is the ith coordinate in Rn and x*i is the derivative of the ith coordinate xi with respect to time. L represents the lagrangian. so using an arbitrary change of coordinates, qi = qi(x1, x2, ..., xn) i...- demonelite123
- Thread
- Coordinate Euler Independent Lagrange
- Replies: 2
- Forum: Beyond the Standard Models
-
E
How Do You Solve a Lagrange Multiplier Problem with a Spherical Constraint?
1. Assume we have function V(x,y,z) = 2x2y2z = 8xyz and we wish to maximise this function subject to the constraint x^2+Y^2+z^2=9. Find the value of V at which the max occurs 2. Function: V(x,y,z) = 2x2y2z = 8xyz Constraint: x^2+Y^2+z^2=9 3. So far I have gone Φ= 8xyz +...- Elliotc
- Thread
- Lagrange Lagrange multiplier
- Replies: 1
- Forum: Calculus and Beyond Homework Help
-
W
Solve problem without Lagrange Equations.
A friend and I were debating the solution to this problem, seen below, and cannot solve it without using Lagrange equations but it is suppose to have a solution that is super simple; but we didn't see it. Anyway, it is a old qualifier question from the Univ. of Wisconsin (open record so...- Wondering
- Thread
- Lagrange
- Replies: 1
- Forum: Advanced Physics Homework Help
-
A
Lagrange multipliers and two constraints
So I need to find the min and max values of f(x,y,z) = x^2 + 2y^2 + 3z^2 given the constraints x + y + z = 1 and x - y + 2z =2. I've gotten as far as (2x, 4y, 6z) = (u,u,u) + (m,-m,2m). I'm stuck trying to solve this system of equations. Any hints?- autre
- Thread
- Constraints Lagrange Lagrange multipliers
- Replies: 5
- Forum: Calculus and Beyond Homework Help
-
L
Maximizing the Lagrangian with Constraints to Solving Problems
Homework Statement L = - \Sigma x,y (P(x,y) log P(x,y)) + \lambda \Sigmay (P(x,y) - q(x)) This is the Lagrangian. I need to maximize the first term in the sum with respect to P(x,y), subject to the constraint in the second term. The first term is a sum over all possible values of x,y...- Legendre
- Thread
- Lagrange Lagrange multiplier
- Replies: 7
- Forum: Calculus and Beyond Homework Help
-
S
Lagrange Multipliers/System of Equations?
Homework Statement I seem to be struggling a bit to understand how my prof solved this problem...I think it might be my diminishing system of equation skills, so forgive me if this doesn't belong in the calc section. Use Lagrange multipliers to find all extrema of the function subject to...- scoobiedoober
- Thread
- Lagrange
- Replies: 5
- Forum: Calculus and Beyond Homework Help
-
S
Analysis problem using the Lagrange Remainder Theorem
Homework Statement Prove that for every pair of numbers x and h, \left|sin\left(x+h\right)-\left(sinx+hcosx\right)\right|\leq\frac{h^{2}}{2} The Attempt at a Solution Let f(x)= \left|sin\left(x+h\right)-\left(sinx-hcosx\right)\right|? and then to center the taylor polynomial around 0...- shan1732
- Thread
- Analysis Lagrange Remainder Remainder theorem Theorem
- Replies: 1
- Forum: Calculus and Beyond Homework Help
-
A
Undergrad Max/Min of f Using Lagrange Multipliers
In a exercise says: Find max a min of f=-x^2+y^2 abaut the ellipse x^2+4y^2=4 i tried -2x=\lambda 2x 2y=\lambda 8y x^2+4y^2-4=0 then \lambda =-1 or \lambda =\frac{1}{4} , but, ¿how i find x,y?- alejandrito29
- Thread
- Lagrange Lagrange multiplier
- Replies: 6
- Forum: Calculus
-
E
How Do Lagrange Multipliers Help Calculate Distance from a Point to a Plane?
URGENT - Lagrange Multipliers Homework Statement :confused: Using the method of lagrange multipliers prove the formula for the distance from a point (a,b,c) to a plane Ax + By + Cz = DThe Attempt at a Solution Using the equation of the form; H(x,y,z,L) = (x-a)^2 + (y -b)^2 +(z-c)^2 + L(Ax...- EEWannabe
- Thread
- Lagrange Lagrange multipliers
- Replies: 5
- Forum: Calculus and Beyond Homework Help
-
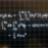
Maximizing f(x,y,z) with Constraint and Lagrange Multipliers
Homework Statement Maximize f(x,y,z)=x^{2}+y^{2}+z^{2} with constraint x^{4}+y^{4}+z^{4}=1 using Lagrange multipliers The Attempt at a Solution I've got the setup as: \Lambda(x,y,z,\lambda)=x^{2}+y^{2}+z^{2}+\lambdax^{4}+\lambday^{4}+\lambdaz^{4}+\lambda I solve for all partials nice...- BeBattey
- Thread
- Lagrange Lagrange multiplier
- Replies: 2
- Forum: Calculus and Beyond Homework Help
-
G
Graduate How Do Satellites Orbit Lagrange Points Without Mass?
Physics gurus: I understood from Newton's Law that a 2 bodies would rotate around their common center of mass. Should one body disappear (Harry Potter invoked here), the other would go flying off at a tangent... like a 'David's Sling" releasing a missile. The mass of the bodies was crucial to...- gregweymann
- Thread
- Lagrange Lagrange points Points
- Replies: 15
- Forum: Special and General Relativity
-
P
How Do You Apply Lagrange Multipliers to Optimize a Function with Constraints?
Let f(x,y)= -2x^2-2xy+y^2+2 Use Lagrange multipliers to find the minimum of f subject to the constraint 4x-y = 6 ∂F / ∂x =..... i got -4x-2y+2y but i coming out as wrong what am i missing ∂F/ ∂Y= ... The function f achieves its minimum, subject to the given constraint, where x =...- peace89
- Thread
- Lagrange Lagrange multiplier
- Replies: 3
- Forum: Calculus and Beyond Homework Help
-
P
Undergrad Max Vol Rect Solid Cut from Sphere: Find Dim & Vol
A rectangular solid of maximum volume is to be cut from a solid sphere of radius r. Determine the dimension of the solid so formed and its volume? I have defined my function F(l,b,h) as lbh, but i don't know how to define my constraint condition from my question- paulojomaje
- Thread
- Lagrange Lagrange multiplier
- Replies: 1
- Forum: Calculus
-
R
How Do You Use Lagrange Multipliers to Maximize Box Volume in an Ellipsoid?
1. Problem Statement: Use Lagrange multipliers to find the volume of the largest box with faces parallel to the coordinate system that can be inscribed in the ellipsoid: 6x2 + y2 + 3z2 = 2 2. Homework Equations : f(x,y,z) = \lambdag(x,y,z) 3. Attempt at a solution f(x,y,z) is the...- ryan8888
- Thread
- Lagrange Lagrange multiplier
- Replies: 5
- Forum: Advanced Physics Homework Help
-
F
Lagrange Multiplier /w Mixed Inequality/Equality Constraints
Homework Statement Find the extreme values of the function f(x,y,z) = xy + z^2 in the set S:= { y\geq x, x^2+y^2+z^2=4 } Homework Equations The Attempt at a Solution Ok, so This is clearly a lagrange multiplier question. Geometrically, I can see that the region that is the constraint is...- fission14
- Thread
- Constraints Lagrange Lagrange multiplier Mixed
- Replies: 1
- Forum: Calculus and Beyond Homework Help
-
O
Maximize f(x,y,z) with Lagrange Multipliers
Find the maximum value of f(x,y,z) = 5xyz subject to the constraint of [PLAIN]http://www3.wolframalpha.com/Calculate/MSP/MSP9619f6019f3fia87i60000567g3gb3dhi833if?MSPStoreType=image/gif&s=6&w=126&h=20. I know to find the partial derivatives of the function and the constraint. Then, set up...- Oglethorpe
- Thread
- Lagrange Lagrange multiplier
- Replies: 2
- Forum: Calculus and Beyond Homework Help
-
K
How Do You Solve Lagrange Multipliers with Complex Constraints?
1. Use the method of Lagrange multipliers to nd the minimum value of the function: f(x,y,z) = xy + 2xz + 2yz subject to the constraint xyz = 32. I understand the method how Lagranges Multipliers is donw done but seem to have got stuck solving the Simultaneous Equations involving the...- kawsar
- Thread
- Bit Lagrange Lagrange multipliers Stuck
- Replies: 8
- Forum: Calculus and Beyond Homework Help
-
H
More fun with lagrange multipliers
Homework Statement Find the point closest to the origin on the line of intersection of the planes y + 2z = 12 and x + y = 6Homework Equations \nuf = \lambda\nug1 +\mu\nug2 f = x2+y2+z2 g1: y + 2z = 12 g2: x + y = 6 There are supposed to be gradients on all of those, whether or not LaTeX...- hiigaranace
- Thread
- Fun Lagrange Lagrange multipliers
- Replies: 6
- Forum: Calculus and Beyond Homework Help
-
H
Recursive Lagrange multipliers
Hey all, this is my first post, so I apologize in advance if data are missing/format is strange/etc. I'm working with lagrange multipliers, and I can get to the answer about half the time. The problem is, I'm not really sure how to deal with things when the multiplier equation becomes...- hiigaranace
- Thread
- Lagrange Lagrange multipliers
- Replies: 5
- Forum: Calculus and Beyond Homework Help
-
M
Graduate Euler Lagrange equation - weak solutions?
Hello there, I was wondering if anybody could indicate me a reference with regards to the following problem. In general, the Euler - Lagrange equation can be used to find a necessary condition for a smooth function to be a minimizer. Can the Euler - Lagrange approach be enriched to cover...- muzialis
- Thread
- Euler Euler lagrange equation Lagrange Lagrange equation Weak
- Replies: 1
- Forum: Differential Equations
-
S
Finding Minimum with Lagrange Multipliers
Homework Statement Find the minimum of f(x,y) = x^2 + y^2 subject to the constraint g(x,y) = xy-3 = 0 Homework Equations delF = lambda * delG The Attempt at a Solution Okay, after lecture, reviewing the chapter and looking at some online information, this is what I have so far...- smashyash
- Thread
- Lagrange Lagrange multipliers
- Replies: 17
- Forum: Calculus and Beyond Homework Help
-
M
Graduate How can I find the y(x) that minimizes the functional J?
Hello there, I am dealing with the functional (http://en.wikipedia.org/wiki/First_variation) J = integral of (y . dy/dx) dx When trying to compute the Euler Lagrange eqaution I notice this reduces to a tautology, i.e. dy/dx - dy/dx = 0 How could I proceed for finding the y(x) that... -
R
Math Physics: Lagrange Multiplier question
Homework Statement Hello. I've been stuck on a Lagrange Multiplier problem. It's from Mathematical Methods in the Physical Sciences by Mary Boas 3rd edition pg. 222. The question is: What proportions will maximize the volume of a projectile in the form of a circular cylinder with one conical...- randomperson8
- Thread
- Lagrange Lagrange multiplier Physics
- Replies: 1
- Forum: Introductory Physics Homework Help
-
C
Graduate Solve Highest/Lowest Points on Curve of Intersection with Lagrange Multipliers
Hi There I would like help on a question about Lagrange multipliers. Question: Consider the intersection of two surfaces: an elliptic paraboloid z=x^2 + 2*x + 4*y^2 and a right circular cylinder x^2 + y^2 = 1. Use Lagrange multipliers to find the highest and lowest points on the curve of the... -
B
Graduate Lagrangian mechanics - Euler Lagrange Equation
Euler Lagrange Equation : if y(x) is a curve which minimizes/maximizes the functional : [SIZE="4"]F\left[y(x)\right] = \int^{a}_{b} [SIZE="4"]f(x,y(x),y'(x))dx then, the following Euler Lagrange Differential Equation is true. \frac{\partial}{\partial x} [SIZE="4"]-... -
K
Graduate Why Does the Missing Lagrange Multiplier Matter in Differential Forms?
I think that many of us have had to endure working with Lagrange multipliers in the past, but it seems to me that it has always been taught incorrectly. So the statement (if you will allow me to use differential forms) is Now my issue is that it's well-known that this should be... -

Euler-Lagrange Equation for a Stationary Action
Homework Statement If L(y, y', x) = y^{2} + y'^{2} then find the appropriate Euler Lagrange Equation. I have absolutely no idea how to solve this. I used the differential form of the Euler Lagrange equations for a stationary action but the answer i got was nothing like the answer in the book...- WannabeNewton
- Thread
- Euler Lagrange
- Replies: 2
- Forum: Calculus and Beyond Homework Help
-
P
3D pendulum-spring-damper (Lagrange)
[PLAIN]http://img337.imageshack.us/img337/3623/pensp.jpg Homework Statement I need to find the equations of motions via Lagrange's formulation when the generalized coordinates are: \vec{q}=[x,y,z]^T2. The attempt at a solution I need to verify whether what I obtained so far is true or not...- PhMichael
- Thread
- 3d Lagrange
- Replies: 1
- Forum: Advanced Physics Homework Help
-
R
Taylor Polynomials- Lagrange remainder
So I'm studying for a final, and it just so happens my professor threw taylor polynomials at us in the last week.. I understand the concept of a taylor polynomial but i need some help fully understand the LaGrange remainder theorem if we have a function that has n derivatives on the interval...- rambo5330
- Thread
- Lagrange Polynomials Remainder Taylor
- Replies: 3
- Forum: Calculus and Beyond Homework Help
-
D
Lagrange Multipliers: A theoretical question and an example
Hello physicsforums community. I have recently learned about Lagrange multipliers and have been given three problems to solve. Could you guys please go over my work and see if I have the gist of it? One question, a theoretical one, I have no idea how to begin. Any advice regarding this would be...- diewolke
- Thread
- Example Lagrange Lagrange multipliers Theoretical
- Replies: 1
- Forum: Calculus and Beyond Homework Help
-
S
Lagrange to find eigen values and vectors?
Homework Statement im given a matrix A= 1 -2 ///////////////////////-2 4 im told to find the eigen values and the vectors... but the thing is i have never came across this, i learned lagrange multipliers but never used it to find eigen values and vector.. Homework Equations The...- seto6
- Thread
- Eigen values Lagrange Vectors
- Replies: 4
- Forum: Calculus and Beyond Homework Help
-
U
Lagrange multipliers: Variables cancelling out?
Find the maximum and minimum of f(x,y)=y2-x2 with the constraint x2/4 +y2=2. My calculus professor gave us this on his exam and there were no problems like this in the book and I would just like to know how it's done because it's bothering me ha. After doing the partial derivatives I got...- ucbearcat
- Thread
- Cancelling Lagrange Lagrange multipliers Variables
- Replies: 1
- Forum: Calculus and Beyond Homework Help
-
T
Lagrange Multipliers Find 3 positive numbers?
Homework Statement Find 3 positive numbers x, y and z for which: their sum is 24 and which maximizes the product: P = x2y3z. Find the maximum product. The Attempt at a Solution Ok, I know how to set up the equations. x + y + z = 24 Delta(F) <2xy3z, 2x2y2z, x2y3> fx = 2xy3z...- tak13
- Thread
- Lagrange Lagrange multipliers Numbers Positive
- Replies: 1
- Forum: Calculus and Beyond Homework Help
-
D
Lagrange constraint mechanics problem
http://img221.imageshack.us/img221/3754/capturetp.png Just a simple question. I can see that for this to work I need: Trot = 1/5 ma2(thetaDOT + phiDOT)2 Just can't work out what phi has to do with rotational kinetic energy. I would have thought it would need to be simply the same thing but...- DylanG
- Thread
- Constraint Lagrange Mechanics
- Replies: 1
- Forum: Advanced Physics Homework Help
-
L
Graduate Interpolation using Lagrange polynomials
Problem: We want to calculate a polynomial of degree N-1 that crosses N known points in the plane. Solution A: solving a NxN system of linear equation (Gauss elimination) Solution B: construction from Lagrange basis polynomials. One of my professors said that the first solution is...- Lojzek
- Thread
- Interpolation Lagrange Polynomials
- Replies: 1
- Forum: General Math
-
B
Question of lagrange theorem converse.
Homework Statement Let G be an abelian group. Suppose p divides ord(G) where p is prime no. Prove G has a subgroup of order p. Homework Equations lagrange theorem converse The Attempt at a Solution i know the converse is lagrange theorem and easy and this is not the case. I know...- betty2301
- Thread
- Lagrange Theorem
- Replies: 1
- Forum: Calculus and Beyond Homework Help
-
S
Finding Minimum Values with Lagrange Multipliers
Homework Statement Minimise = x2 + y2 subject to C(x,y) = 4x2 + 3y2 = 12. Homework Equations The Attempt at a Solution I let h(x,y) = x2 + y2 + \lambda(4x2 + 3y2 - 12). I got hx = 2x + 8\lambdax = 0, hy = 2y + 6\lambday = 0, but here I get 2 values of \lambda, \lambda = -1/4 &...- squenshl
- Thread
- Lagrange Lagrange multipliers
- Replies: 13
- Forum: Calculus and Beyond Homework Help
-
D
Lagrange Multipliers: Advantages & Necessity?
I do not have one specific question that needs answering. Rather, it is about Lagrange multipliers in general. So for certain minimization/maximization questions (ie find the shortest distance from some point to some plane) it seems that one could solve the question using lagrange multipliers...- DR13
- Thread
- Lagrange Lagrange multipliers
- Replies: 4
- Forum: Calculus and Beyond Homework Help
-
T
Lagrange Multipliers Question?
Lagrange Multipliers Question? Homework Statement Find the minimum and maximum values of the function subject to the given constraint. f (x,y,z) = x^2 - y - z, x^2 - y^2 +z = 0 The Attempt at a Solution Okay this is what I did: Gradient f = <2x,-1,-1> Gradient g =...- TheSpaceGuy
- Thread
- Lagrange Lagrange multipliers
- Replies: 7
- Forum: Calculus and Beyond Homework Help
-
C
Graduate Lagrange Points, Maximum mass and their effects
So, I'm working through some ideas dealing with Lagrange points. I understand that, the rotation and mass of 2 objects in space create stable areas where an object of "insignificant Mass" compared to the objects it's balancing against, allows for the placement of an object in a stable area...- Chand-Ashoka
- Thread
- Effects Lagrange Lagrange points Mass Maximum Points
- Replies: 8
- Forum: Astronomy and Astrophysics