Saladsamurai
- 3,009
- 7
1-D Conduction+Convection::Deriving a Finite Difference Scheme
***For those of you who would like to skip the derivation of the energy balance, skip ahead to the bold subheading below where the actual Finite Difference Scheme begins***
I am trying to derive a finite difference scheme for 1-Dimensional conduction and convection. I am using a similar approach to one used in my lecture notes for conduction only. It is a control volume approach to this.
I would upload a picture, but I think the 1D case is simple enough to picture. Picture a bar with constant cross-sectional area. We will work with a cross-sectional "slice" of the bar whose length is dx
EDIT: Picture added
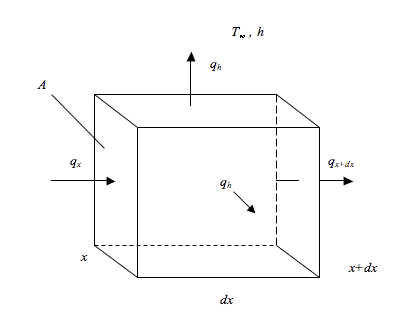
So as said, there is conduction occurring (i.e. a temperature gradient is present) and there is convection going on. Here are the properties of the bar [with dimensions]:
A = constant cross-sectional area [Length2]
K = thermal conductivity [Power/(Length-Temp)]
c = specific heat capacity [Energy/(Mass-Temp)]
h = convective coefficient of heat transfer [Power/(Length2-Temp)]
\rho = density [Mass/Length3]The Energy balance is given by:
E_{in} + E_{generated} = \Delta U +E_{out}\qquad(1)
There is a conduction term on the left edge of the control volume at x and a conduction term at the right edge at x + dx
That is, the energy balance becomes:
q_xA\,dt+QA\,dx\,dt=\Delta U+q_{x+dx}A\,dt + q_hP\,dx\,dt \qquad (2)
where:
q_x is the heat conducted (heat flux) into the control volume (CV) at the surface edge x.
q_{x+dx} is the heat conducted (heat flux) out of the control volume at the surface edge x+dx.
Q is the internal heat source (or sink); heat generated (or removed) per unit volume.
q_h = h(T-T_{\infty}) is the convective heat transfer
P is the perimeter around the constant cross-sectional area A
Presumably they have neglected convective heat transfer (HT) at the end faces and are only considering HT via the body's surface area *though I am not sure why ~ Any thoughts on that?).
So here goes the derivation:
first we note that the conductive term at x is given by Fourier's law of conduction:
q_x = -K_{xx}\frac{dT}{dx} \qquad (3)
Using a two-term Taylor series, we can expand the q_{x+dx} term to be:
<br /> q_{x+dx} = -[K_{xx}\frac{dT}{dx}+\frac{d}{dx}(K_{xx}\frac{dT}{dx})\,dx] \qquad (4)<br />
plugging (3) and (4) into (2) yields:
-K_{xx}\frac{dT}{dx}A\,dt+QA\,dx\,dt=\Delta U-[K_{xx}\frac{dT}{dx}+\frac{d}{dx}(K_{xx}\frac{dT}{dx})\,dx]A\,dt + q_hP\,dx\,dt <br /> \qquad (5)
Canceling the -K_{xx}\frac{dT}{dx}A\,dt term of both sides and then dividing through by A*dx*dt and noting that \Delta U = c\rho A\,dT\,dx and assuming that Kxx is constant yields:
K\frac{\partial{}^2 T}{\partial{x}^2} + Q = \rho c \frac{\partial{T}}{\partial{t}} +\frac{hP}{A}(T - T_{\infty}) \qquad (6)
or for no source term we have:
\frac{\partial{}^2 T}{\partial{x}^2} =\frac{ \rho c}{K}\, \frac{\partial{T}}{\partial{t}}+\frac{hP}{AK}(T - T_{\infty}) \qquad (7)*****************************************************************************
*****************************************************************************
Now for the finite difference scheme:
If we have a one dimensional bar we want to find the temperature at a point 'p' that is located equidistant in the x-direction to points 'p+1' and 'p-1.' We can rewrite the derivative terms via Taylor expansions; that is,
\frac{\partial{}^2 T}{\partial{x}^2} \approx \frac{T(x+dx) - 2T(x) + T(x-dx)}{dx^2}<br /> \qquad (8)
and
\frac{\partial{T}}{\partial{t}} \approx \frac{T(t+dt)-T(t)}{dt}\qquad (9)
Hence, (7) becomes:
\frac{T(x+dx) - 2T(x) + T(x-dx)}{dx^2}} =\frac{ \rho c}{K}\, \frac{T(t+dt)-T(t)}{dt}+\frac{hP}{AK}(T - T_{\infty}) \qquad (10)
EQUATION (10) is where I am a little confused. I don't think that these should be "total derivatives" but instead should be "partials" but as engineers, we like to abuse notation. So I would like to fix this (any thoughts are helpful).
Looking at the right-hand-side of (10) there are 2 "T" terms I need to work out. Is the "(T+dt)-term" at location "x" ? I believe it is. And is the convection "T-term" at time "t" ? I also believe that is true.
If so, I am going to let T(x) at time "t" be represented by T_p^t similarly T(x,t+dt) would be represented by T_p^{t+dt} and so on.
With this notation, we can represent equation (10) as:
T_{p+1} - 2T_p + T_{p-1} =(\frac{ dx^2\rho c}{K})\, \frac{T^{t+dt}_p-T_p^t}{dt}+(\frac{dx^2\,hP}{AK})(T_p^t - T_{\infty}) \qquad (11)
Now we have purposefully left the time dependence off of the T-terms on the left hand side as this will determine whether the scheme is explicit or implicit --that is whether it is evaluated at 't' or 't+dt'
I am still unsure of the "T" on the right-hand-side in the brackets (T_p^t - T_{\infty}).
Should I have left the time dependence ambiguous on that as well? And define it when I define the scheme type? And is it indeed at point 'p' (pretty sure it is)?
***For those of you who would like to skip the derivation of the energy balance, skip ahead to the bold subheading below where the actual Finite Difference Scheme begins***
I am trying to derive a finite difference scheme for 1-Dimensional conduction and convection. I am using a similar approach to one used in my lecture notes for conduction only. It is a control volume approach to this.
I would upload a picture, but I think the 1D case is simple enough to picture. Picture a bar with constant cross-sectional area. We will work with a cross-sectional "slice" of the bar whose length is dx
EDIT: Picture added
So as said, there is conduction occurring (i.e. a temperature gradient is present) and there is convection going on. Here are the properties of the bar [with dimensions]:
A = constant cross-sectional area [Length2]
K = thermal conductivity [Power/(Length-Temp)]
c = specific heat capacity [Energy/(Mass-Temp)]
h = convective coefficient of heat transfer [Power/(Length2-Temp)]
\rho = density [Mass/Length3]The Energy balance is given by:
E_{in} + E_{generated} = \Delta U +E_{out}\qquad(1)
There is a conduction term on the left edge of the control volume at x and a conduction term at the right edge at x + dx
That is, the energy balance becomes:
q_xA\,dt+QA\,dx\,dt=\Delta U+q_{x+dx}A\,dt + q_hP\,dx\,dt \qquad (2)
where:
q_x is the heat conducted (heat flux) into the control volume (CV) at the surface edge x.
q_{x+dx} is the heat conducted (heat flux) out of the control volume at the surface edge x+dx.
Q is the internal heat source (or sink); heat generated (or removed) per unit volume.
q_h = h(T-T_{\infty}) is the convective heat transfer
P is the perimeter around the constant cross-sectional area A
Presumably they have neglected convective heat transfer (HT) at the end faces and are only considering HT via the body's surface area *though I am not sure why ~ Any thoughts on that?).
So here goes the derivation:
first we note that the conductive term at x is given by Fourier's law of conduction:
q_x = -K_{xx}\frac{dT}{dx} \qquad (3)
Using a two-term Taylor series, we can expand the q_{x+dx} term to be:
<br /> q_{x+dx} = -[K_{xx}\frac{dT}{dx}+\frac{d}{dx}(K_{xx}\frac{dT}{dx})\,dx] \qquad (4)<br />
plugging (3) and (4) into (2) yields:
-K_{xx}\frac{dT}{dx}A\,dt+QA\,dx\,dt=\Delta U-[K_{xx}\frac{dT}{dx}+\frac{d}{dx}(K_{xx}\frac{dT}{dx})\,dx]A\,dt + q_hP\,dx\,dt <br /> \qquad (5)
Canceling the -K_{xx}\frac{dT}{dx}A\,dt term of both sides and then dividing through by A*dx*dt and noting that \Delta U = c\rho A\,dT\,dx and assuming that Kxx is constant yields:
K\frac{\partial{}^2 T}{\partial{x}^2} + Q = \rho c \frac{\partial{T}}{\partial{t}} +\frac{hP}{A}(T - T_{\infty}) \qquad (6)
or for no source term we have:
\frac{\partial{}^2 T}{\partial{x}^2} =\frac{ \rho c}{K}\, \frac{\partial{T}}{\partial{t}}+\frac{hP}{AK}(T - T_{\infty}) \qquad (7)*****************************************************************************
*****************************************************************************
Now for the finite difference scheme:
If we have a one dimensional bar we want to find the temperature at a point 'p' that is located equidistant in the x-direction to points 'p+1' and 'p-1.' We can rewrite the derivative terms via Taylor expansions; that is,
\frac{\partial{}^2 T}{\partial{x}^2} \approx \frac{T(x+dx) - 2T(x) + T(x-dx)}{dx^2}<br /> \qquad (8)
and
\frac{\partial{T}}{\partial{t}} \approx \frac{T(t+dt)-T(t)}{dt}\qquad (9)
Hence, (7) becomes:
\frac{T(x+dx) - 2T(x) + T(x-dx)}{dx^2}} =\frac{ \rho c}{K}\, \frac{T(t+dt)-T(t)}{dt}+\frac{hP}{AK}(T - T_{\infty}) \qquad (10)
EQUATION (10) is where I am a little confused. I don't think that these should be "total derivatives" but instead should be "partials" but as engineers, we like to abuse notation. So I would like to fix this (any thoughts are helpful).
Looking at the right-hand-side of (10) there are 2 "T" terms I need to work out. Is the "(T+dt)-term" at location "x" ? I believe it is. And is the convection "T-term" at time "t" ? I also believe that is true.
If so, I am going to let T(x) at time "t" be represented by T_p^t similarly T(x,t+dt) would be represented by T_p^{t+dt} and so on.
With this notation, we can represent equation (10) as:
T_{p+1} - 2T_p + T_{p-1} =(\frac{ dx^2\rho c}{K})\, \frac{T^{t+dt}_p-T_p^t}{dt}+(\frac{dx^2\,hP}{AK})(T_p^t - T_{\infty}) \qquad (11)
Now we have purposefully left the time dependence off of the T-terms on the left hand side as this will determine whether the scheme is explicit or implicit --that is whether it is evaluated at 't' or 't+dt'
I am still unsure of the "T" on the right-hand-side in the brackets (T_p^t - T_{\infty}).
Should I have left the time dependence ambiguous on that as well? And define it when I define the scheme type? And is it indeed at point 'p' (pretty sure it is)?
Last edited:
