Electric heat generation from parallel rods carrying current in an oil bath

[jackkk_gatz]

Homework Statement

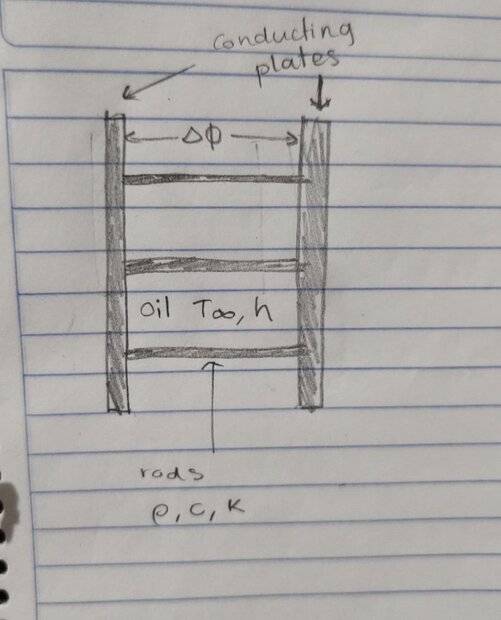
Two parallel conducting plates have a high potential difference $\Delta \phi$ and are held by a bundle of rods of circular cross section with length L and radius R where L>>R. Each rod is not a perfect electrical insulator, and has an electrical resistivity (not to be confused with electrical resistance) as a linear function of temperature $\rho_e=\rho_{e,0}+\beta*(T-T_0)$, where $\rho_(e,0), T_0, \beta$ are constant values. Since the clamping rods are not perfect electrical insulators, heat generation by electrical conduction is induced along the rod, which is prevented by the continuous circulation of an oil flow which has a bulk temperature $T_\infty$ and a convective heat transfer coefficient h over the rods. On the other hand, it has been established that the thermophysical properties of the rods are not strongly affected by the temperature variation along it: density, specific heat capacity, thermal conductivity. To facilitate the solution of the problem, consider that the plates are in thermal equilibrium with the oil flow. Establish the mathematical model that describes the equilibrium the energy balance along the rod as a function of temperature and the physical and geometrical properties indicated.

Relevant Equations

?

I know that $\dot e_{gen} = \frac {R_{e}i^2} {\pi r^2 L}$ the thing is I don't know the value of i. I didn't write it, but another thing that the problem asks is to determine the flow of electric current. The model I came up with using heat generation due to electrical current is $$ \frac {d(A \frac {dT} {dx})} {dx}+\frac {(\Delta \phi)^2} {(\rho_{e,0}+\beta*(T-T_0))*Akr^2}-\frac {hP} {kA}*(T-T_\infty)=0$$ which i think is overly complicated. So even though the problem states there is heat generation, should i ignore it when obtaining my model? Another thing that I know for sure is i have to find the electric current this way $i=\frac {(\Delta \phi)} {(\rho_{e,0}+\beta*(T-T_0))}$ , i'd expect to find the temperature distribution for T and then substitute it on here $i=\frac {(\Delta \phi)} {(\rho_{e,0}+\beta*(T-T_0))}$ but in order to obtain the temperature distribution i have to establish my mathematical model. So i'm starting to think i should work with $$ \frac {d(A \frac {dT} {dx})} {dx}-\frac {hP} {kA}*(T-T_\infty)=0$$ the thing is that here, on this model, it appears that there is no heat generation. But still im not sure of what to do, I don't know for sure if i'm not ignoring something. Another thing, why is it mentioned in the problem that the rods are not perfect electrical insulators? Why is that important? shouldn't there be heat generation anyway?

 

[haruspex]

I know that $\dot e_{gen} = \frac {R_{e}i^2} {\pi r^2 L}$

Shouldn’t the L be in the numerator?

The model I came up with using heat generation due to electrical current is

You have a dT/dx term. For what reason would the temperature come to vary along a rod if it starts off at a uniform temperature?
Of course, in practice, different rods will be at different temperatures because of the convection currents, but you will have to overlook that.

Treat a rod as being at a uniform steady temperature. What power balance equation can you write?

 

[jackkk_gatz]

Shouldn’t the L be in the numerator?

You have a dT/dx term. For what reason would the temperature come to vary along a rod if it starts off at a uniform temperature?
Of course, in practice, different rods will be at different temperatures because of the convection currents, but you will have to overlook that.

Treat a rod as being at a uniform steady temperature. What power balance equation can you write?

I picked up that formula from the book Heat transfer by Cengel. L is in the denominator because what the formula is doing is computing the volumetric heat, so the volume for the cylinder is the one on the denominator.

And the rod, I believe, that the temperature changes along the rod due to volumetric heat. The rods are acting as fins with constant cross sectional area. So they are dissipating heat. And there is a maximum on the center of the rod, so $\frac {dT}{dx}=0$ when x=L/2

 

[haruspex]

L is in the denominator because what the formula is doing is computing the volumetric heat

I am assuming $R_e$ is the resistivity. If so, the resistance of a rod is proportional to its length and inversely proportional to its cross section: $R=\frac{R_eL}{\pi r^2}$. The power produced in the rod is $\frac{V^2}R=\frac{V^2\pi r^2}{R_eL}$.

the temperature changes along the rod due to volumetric heat. The rods are acting as fins with constant cross sectional area. So they are dissipating heat.

I don't see how that leads to temperature varying along a rod. Rather, it means it varies across the radius of a rod. This makes it quite tricky. It means the current density will be lower near the centre because the higher temperature gives it higher resistance.
You will need to model a rod as concentric cylindrical elements.

 

[jackkk_gatz]

I am assuming $R_e$ is the resistivity. If so, the resistance of a rod is proportional to its length and inversely proportional to its cross section: $R=\frac{R_eL}{\pi r^2}$. The power produced in the rod is $\frac{V^2}R=\frac{V^2\pi r^2}{R_eL}$.

I don't see how that leads to temperature varying along a rod. Rather, it means it varies across the radius of a rod. This makes it quite tricky. It means the current density will be lower near the centre because the higher temperature gives it higher resistance.
You will need to model a rod as concentric cylindrical elements.

Oh okay R in this case is resistance, the symbol used for resistivity is $\rho$.

And about the other thing, I see possible that temperature varies across the radius. But the problem mentiones that L>>R so I think I should give more importance to the length, as if the temperature variation across the radius might be small. And for the temperature varying along the rod, well, if there is volmetric heat generation, lets say constant all along the rod, the conducting plates might act as heat sinks. So the extremes would be colder and as we aproach the center it would get hotter, thats how i see it. The heat would have a a harder time making it out if its far away from the conducting plates, causing heating, which might be dissipated with the oil flow.

 

[haruspex]

the conducting plates might act as heat sinks

Indeed they might, but you are given no suitable information on that, so you will have to assume not.

 

[jackkk_gatz]

Indeed they might, but you are given no suitable information on that, so you will have to assume not.

hmm okayy, I think I understand now. I have a question, when the problem ask me to obtain axial temperature profile, what does it mean axial? Along the rod? In the radial direction?

 

[jackkk_gatz]

This is the rest of things the problem asks for, in case it is important:

Establish a mathematical model describing the energy balance along the rod as a function of temperature and the indicated physical and geometrical properties (do not forget the boundary conditions). In steady state obtain the axial temperature profile as well as its maximum value. Calculate the heat flux dissipated by each rod. Determine the electric current flow through each rod, considering that the electric flow develops homogeneously in the whole cross section of the rod and that the electric potential difference is constant.

 

[haruspex]

when the problem ask me to obtain axial temperature profile, what does it mean axial? Along the rod? In the radial direction?

It means radial.

considering that the electric flow develops homogeneously

Ouch. I had assumed this was all for steady state. You will need equations for how the temperature changes at radius r as power is dissipated there at the same time that heat flows into that cylindrical element from inside and out on the outside.
I think it will help to work in terms of voltage and resistance, avoiding references to current.

 

[haruspex]

Some more hints in case you are still stuck.

You need a differential equation for the temperature of a cylindrical shell as a function of radius and time. For reasons that will become apparent, I will use $\theta$ for temperatures instead of T.

By symmetry, $\theta=\theta(r, t)$. The rate of gain of temperature at a given radius, $\frac{\partial\theta}{\partial t}$ is the sum of two terms. One term is for diffusion of heat from neighbouring cylinders (think $\nabla^2$) and one for locally generated heat per unit volume.
For the latter term, consider the resistance of a cylindrical element, the voltage drop along it and its volume.
You will need constants for conductivity and specific heat per unit volume.

If you need to solve the equation, you might need to make an approximation for small $\beta\Delta\theta$. Using the usual notational convention, then assume $\theta(r,t)=\Sigma R_i(r)T_i(t)$ and apply separation of variables.

 

[Chestermiller]

For the ohm's law equation, you have $$I\rho\frac{dx}{A}=d\phi$$where the current I is constant. So, $$\Delta \phi=\frac{I}{A}\int_0^L{\rho dx}$$and $$I=\frac{A\Delta \phi}{\int_0^L{\rho dx}}$$and the rate of heat generation within the rod between x and x + dx is $$dG=Id\phi=\left(\frac{\Delta \phi}{\int_0^L{\rho dx}}\right)^2\rho Adx$$The heat conduction equation then reads: $$0=k\frac{d^2T}{dx^2}+\left(\frac{\Delta \phi}{\int_0^L{\rho dx}}\right)^2\rho -\frac{4h}{D}(T-T_{\infty})$$

 

[Lnewqban]

This statement seems to be contradictory, to me at least:

Since the clamping rods are not perfect electrical insulators, heat generation by electrical conduction is induced along the rod, which is prevented by the continuous circulation of an oil flow which has a bulk temperature T∞ and a convective heat transfer coefficient h over the rods.