- #1
Math Amateur
Gold Member
MHB
- 3,990
- 48
I am reading David Bachman's book: "A Geometric Approach to Differential Forms" (Second Edition) ...
I need some help with Exercise 3.2, Part 2 ... Exercise 3.2, Part 2 ... reads as follows:View attachment 8607Bachman gives he answer to Exercise 3.2, Part 2 as \(\displaystyle dy = -4dx\) ... ... but ... I cannot understand how he gets this answer ..Can someone please help ...
Peter=========================================================================================It may help MHB
readers of the above post to have access to Bachman's Section 3.2 ... ... so I am providing the same .. ... as follows:View attachment 8608
View attachment 8609
View attachment 8610It may also help MHB
readers of the above post to have access to Bachman's Section 3.1 ... ... so I am providing the same .. ... as follows:View attachment 8611
View attachment 8612
Hope that helps ...
Peter
I need some help with Exercise 3.2, Part 2 ... Exercise 3.2, Part 2 ... reads as follows:View attachment 8607Bachman gives he answer to Exercise 3.2, Part 2 as \(\displaystyle dy = -4dx\) ... ... but ... I cannot understand how he gets this answer ..Can someone please help ...
Peter=========================================================================================It may help MHB
readers of the above post to have access to Bachman's Section 3.2 ... ... so I am providing the same .. ... as follows:View attachment 8608
View attachment 8609
View attachment 8610It may also help MHB
readers of the above post to have access to Bachman's Section 3.1 ... ... so I am providing the same .. ... as follows:View attachment 8611
View attachment 8612
Hope that helps ...
Peter
Attachments
-
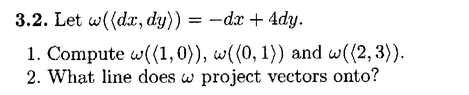 Bachman ... Exercise 3.2 .png3.3 KB · Views: 59
Bachman ... Exercise 3.2 .png3.3 KB · Views: 59 -
 Bachman - 1 - Section 3.1 - PART 1 ... .png26.2 KB · Views: 64
Bachman - 1 - Section 3.1 - PART 1 ... .png26.2 KB · Views: 64 -
 Bachman - 2 - Section 3.1 - PART 2 ... .png40.1 KB · Views: 64
Bachman - 2 - Section 3.1 - PART 2 ... .png40.1 KB · Views: 64 -
 Bachman - 3 - Section 3.1 - PART 3 ... .png26.9 KB · Views: 65
Bachman - 3 - Section 3.1 - PART 3 ... .png26.9 KB · Views: 65 -
 Bachman - 1 - Section 3.0 - PART 1 ... .png20.6 KB · Views: 57
Bachman - 1 - Section 3.0 - PART 1 ... .png20.6 KB · Views: 57 -
 Bachman - 2 - Section 3.0 - PART 2 ... .png75.5 KB · Views: 57
Bachman - 2 - Section 3.0 - PART 2 ... .png75.5 KB · Views: 57