The Indiscrete Topology is Pseudometrizable ... Willard, Example 3.2(d)

[Math Amateur]

TL;DR Summary

I need help in order to make sense of an Example of Stephen Willard's on the trivial topology and the trivial pseudometric ... I find the example confusing ...

I am reading Stephen Willard: General Topology ... ... and am currently focused on Chapter 1: Set Theory and Metric Spaces and am currently focused on Section 2: Metric Spaces ... ...

I need help in order to fully understand Example 3.2(d) ... .. Example 3.2(d) reads as follows:

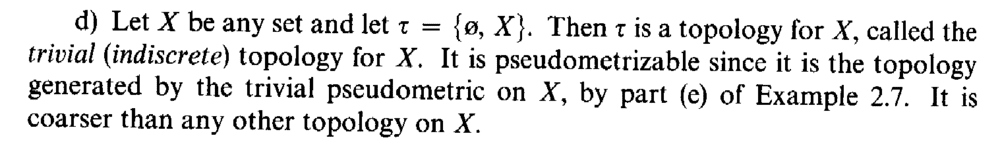and Example 2.7(e) reads as follows:

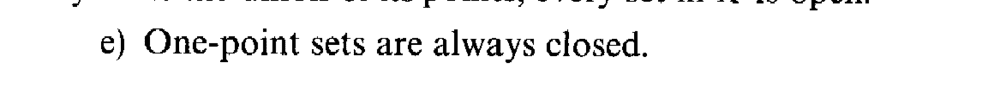In Example 3.2(d) we read the following:

" ... It is pseudometrizable since it is the topology generated by the trivial pseudometric on X, by part (e) of Example 2.7. ... ... "I am somewhat lost by this example ...

Can someone please demonstrate that (X, $\tau$ ) is the topology generated by the trivial pseudometric on X ... and explain the relation to part (e) of Example 2.7. ...Help will be much appreciated ...

Peter

 

[WWGD]

Can you remind us of the meaning of "Pseudometrizable" and "Pseudo metric"?

 

[andrewkirk]

Hello Peter. Good to hear from you. Hope you're managing OK in the current difficult times.

The trivial pseudometric on a space is the one that says the distance between any two points is zero. It is 'pseudo' because a real metric requires a nonzero distance between any distinct points.

The topology generated by a metric is the one generated by the open balls of the metric. An open ball centred on P with radius r is the set of all points with distance less than r from P. Under the trivial pseudometric, for any point P, all points in the space are in every open ball of nonzero radius, because they are all distance zero away!
So the only open balls are the empty set (r=0, P anywhere ) and the universal set (r>0, P anywhere). The topology generated by those two is the trivial topology that consists of just those two open sets.

 

[andrewkirk]

I don't think I agree with (e) that one-point sets are closed. Consider where X = {1, 2}. Under the trivial topology, the open sets are {} and {1, 2}. The closed sets are the complements of those, which are {1, 2} and {}. As you can see, neither of the one-point sets {1} or {2} is open or closed. In the discrete topology - the maximal topology that is in some sense the opposite of the indiscrete/trivial topology - one-point sets are closed, as well as open ("clopen"). That's because the topology is defined by every one-point set being open, and every one-point set is the complement of the union of all the other points. That union is open, so the one-point set is closed.

 

[member 587159]

I don't think I agree with (e) that one-point sets are closed. Consider where X = {1, 2}. Under the trivial topology, the open sets are {} and {1, 2}. The closed sets are the complements of those, which are {1, 2} and {}. As you can see, neither of the one-point sets {1} or {2} is open or closed. In the discrete topology - the maximal topology that is in some sense the opposite of the indiscrete/trivial topology - one-point sets are closed, as well as open ("clopen"). That's because the topology is defined by every one-point set being open, and every one-point set is the complement of the union of all the other points. That union is open, so the one-point set is closed.

I agree with this. In general in any space with 2 or more poinys that has the indiscrete topology (thus only nothing and everything are open sets), no singelton is closed.

 

[Math Amateur]

I don't think I agree with (e) that one-point sets are closed. Consider where X = {1, 2}. Under the trivial topology, the open sets are {} and {1, 2}. The closed sets are the complements of those, which are {1, 2} and {}. As you can see, neither of the one-point sets {1} or {2} is open or closed. In the discrete topology - the maximal topology that is in some sense the opposite of the indiscrete/trivial topology - one-point sets are closed, as well as open ("clopen"). That's because the topology is defined by every one-point set being open, and every one-point set is the complement of the union of all the other points. That union is open, so the one-point set is closed.

Hi Andrew ...

I am fine, thanks ... hope that you are well also ...

Thanks for clarifying the issue ... especially the point of Example 2.7(e) ... that is the part that confused me ...

Peter

 

[Math Amateur]

I agree with this. In general in any space with 2 or more poinys that has the indiscrete topology (thus only nothing and everything are open sets), no singelton is closed.

Thanks Math_QED ...

Appreciate your help ...

Peter