1 pipe branching into 3 pipes, pressure of each branch?

[kingneptune11]

Hello all,

I am a mechanical engineer, graduated just last year. Although I am not working with fluid mechanics right now, I was browsing through my fluids book from school and saw the section on pipe networks. As I was reading, I developed this question which I could not find an answer to in the book.

Please see the attached image below.

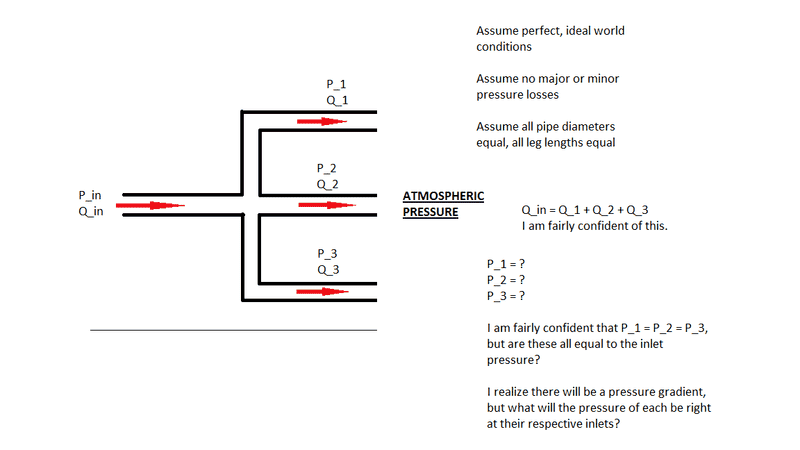
Please note, for my question, let's assume perfect world conditions (all pipes same diameter, all leg lengths are equal, no frictional major/minor losses, etc...)

In the image, you can see we have one inlet, with pressure P_in and flow rate Q_in. My question is about what happens when you branch out into the three branches. I realize that flow rate will split evenly (in a perfect world), but what happens to the pressures?

Keep in mind, the three branches are open to atmosphere. Due to this, I realize there will be a pressure gradient, with the exit pressure reaching 0 (atmosphere). But let's say I am asking about the pressures at each of the branches inlets. Does P_in = P_1 = P_2 = P_3 in an ideal world?

Basically, I have a decent understanding of how flow rates will split when the flow hits the three branches, but how does the pressure of each of the three branches relate to the pressure of the main inlet (P_in)? My hypothesis is that P_in = P_1 = P_2 = P_3, assuming we are talking about the branches inlets (by inlets, I mean where the branches connect to the main pipe).

Thank you for your time and help. Please let me know if I need to further clarify my question. Also, I apologize in advance if this is in the wrong sub-forum. Mods, please move if necessary. Thank you.

 

[256bits]

Hi Kingneptune,

My hypothesis is that P_in = P_1 = P_2 = P_3,

What do you have in your arsenal of knowledge of mechanical engineering that will support or reject your hypothesis?

( Assume you are at site for your employer making the big bucks. There is a real life problem with welds of the pipes breaking at the connections and you are being asked to verify the piping network, starting with stresses from pressure. Do you tell your employer that this wasn't covered in the textbook? )

 

[kingneptune11]

Hi Kingneptune,

What do you have in your arsenal of knowledge of mechanical engineering that will support or reject your hypothesis?

( Assume you are at site for your employer making the big bucks. There is a real life problem with welds of the pipes breaking at the connections and you are being asked to verify the piping network, starting with stresses from pressure. Do you tell your employer that this wasn't covered in the textbook? )

You are correct, I certainly cannot tell him/her that.

I would support this hypothesis by saying that according to Bernoullis Principle, energy in a stream is conserved - meaning that the total energy contained in our volume of air will stay the same (assuming no losses). So, knowing that our total energy must stay the same, and the velocities split evenly, the pressure must stay the same in each pipe. If they didn't, this would indicate a loss or gain of energy.

Is this the correct way of thinking about it? I am still confused to be perfectly honest.

Here's something that is really confusing me - since the velocities in each of the branches are slower than the original inlet velocity, wouldn't we actually see a pressure increase in the branches due to Bernoullis principle? Bernoullis principle say that in a streamline, a decrease in velocity will result in an increase in pressure. So according to this, P1=P2=P3, any of which are greater than P_in. Does this check out?

 

[256bits]

m]\

You are correct, I certainly cannot tell him/her that.

I didn't mean to be harsh, but that is just me. If the boss is your wife and she has the task for you of irrigating the flower bed, the consultation with buddies down at the ports bar to discuss the issue works fine. But ONLY ONCE. they catch on fast.

I would support this hypothesis by saying that according to Bernoullis Principle, energy in a stream is conserved - meaning that the total energy contained in our volume of air will stay the same (assuming no losses). So, knowing that our total energy must stay the same, and the velocities split evenly, the pressure must stay the same in each pipe. If they didn't, this would indicate a loss or gain of energy.

These principles seems reasonable as a first approximation.

Is this the correct way of thinking about it? I am still confused to be perfectly honest.

Here's something that is really confusing me - since the velocities in each of the branches are slower than the original inlet velocity, wouldn't we actually see a pressure increase in the branches due to Bernoullis principle? Bernoullis principle say that in a streamline, a decrease in velocity will result in an increase in pressure. So according to this, P1=P2=P3, any of which are greater than P_in. Does this check out?

Let's ask Bernouliis.
Bernoulli says that since by continuity Vin = 3 V₁ = 3V₂ = 3V₃
Energy from the velocity head E_Vin = 9 E_V1

The energy from the dynamic pressure in 9 times as great in the inlet pipe as in the 3 exiting pipes.
As you have stated, conservation of energy will apply. As the dynamic head ( from the velocity ) has decreased, the hydraulic head ( from the pressure head and elevation ) has to increase. Barring the neglected minor exit/entrance losses at the pipe branching.

You could also replace the 3 exiting lines with one larger pipe of the same area, and connect that to the inlet pipe. Sometimes a simplification works wonders to see things more clearly.

What is it again you were saying about being confused...I must have missed something. :)

 

[kingneptune11]

m]\

I didn't mean to be harsh, but that is just me. If the boss is your wife and she has the task for you of irrigating the flower bed, the consultation with buddies down at the ports bar to discuss the issue works fine. But ONLY ONCE. they catch on fast.

These principles seems reasonable as a first approximation.Let's ask Bernouliis.
Bernoulli says that since by continuity Vin = 3 V₁ = 3V₂ = 3V₃
Energy from the velocity head E_Vin = 9 E_V1

The energy from the dynamic pressure in 9 times as great in the inlet pipe as in the 3 exiting pipes.
As you have stated, conservation of energy will apply. As the dynamic head ( from the velocity ) has decreased, the hydraulic head ( from the pressure head and elevation ) has to increase. Barring the neglected minor exit/entrance losses at the pipe branching.

You could also replace the 3 exiting lines with one larger pipe of the same area, and connect that to the inlet pipe. Sometimes a simplification works wonders to see things more clearly.

What is it again you were saying about being confused...I must have missed something. :)

I think this helped, thank you. So essentially, since the flow through the main pipe and through all three branches in considered one "stream", the energy at anyone point in the stream has to be the same at all the other points, correct? This means, as you said, that when the flow splits off into one of the branches, the dynamic head decreases, so to keep the energy constant, the static head increases? So essentially, our total pressure remains constant throughout the entire stream anywhere in the system? E.g., the total pressure in the main pipe is the same as the total pressure in anyone of the three branches. Am I understanding this correctly? Fascinating subject.

 

[Rocket Scientist]

If we are talking about total pressure (P_total=P_static+P_dynamic), then in the real world, P_in=P_1=P_2=P_3 only if Q_in=Q_1=Q_2=Q_3=0. If you have flow, then by necessity, for total pressure P_in>[any P downstream of the inlet].

If you are neglecting losses, then yes for total pressure P_in=P_1=P_2=P_3 for any Q. If you are talking about static pressure though (what one might measure with a pressure gauge), and the flow areas of your inlet leg and each of the 3 branch legs are equal, then we can calculate the pressure in the branches as a function of the pressure at the inlet, the volumetric flow at the inlet (Q_in), the flow areas (A), and the density of the fluid (rho) as follows:

We start with the equation for total pressure P_total=P_static+P_dynamic and we'll call P_total Pt and P_static Ps, and P_dynamic=1/2* rho*velocity^2

Next we note that velocity=Q/Flow Area, and that since the flow areas are the same Q_in=3*Q_1=3*Q_2=3*Q_3 as pointed out in a previous post.

Now if we do the algebra, we find that Ps_1=Ps_2=Ps_3=Ps_in+(4/9)*rho*(Q_in/A)^2 and yes it is higher in the branches than in the inlet line in order to maintain a constant total pressure throughout.

 

[kingneptune11]

If we are talking about total pressure (P_total=P_static+P_dynamic), then in the real world, P_in=P_1=P_2=P_3 only if Q_in=Q_1=Q_2=Q_3=0. If you have flow, then by necessity, for total pressure P_in>[any P downstream of the inlet].

If you are neglecting losses, then yes for total pressure P_in=P_1=P_2=P_3 for any Q. If you are talking about static pressure though (what one might measure with a pressure gauge), and the flow areas of your inlet leg and each of the 3 branch legs are equal, then we can calculate the pressure in the branches as a function of the pressure at the inlet, the volumetric flow at the inlet (Q_in), the flow areas (A), and the density of the fluid (rho) as follows:

We start with the equation for total pressure P_total=P_static+P_dynamic and we'll call P_total Pt and P_static Ps, and P_dynamic=1/2* rho*velocity^2

Next we note that velocity=Q/Flow Area, and that since the flow areas are the same Q_in=3*Q_1=3*Q_2=3*Q_3 as pointed out in a previous post.

Now if we do the algebra, we find that Ps_1=Ps_2=Ps_3=Ps_in+(4/9)*rho*(Q_in/A)^2 and yes it is higher in the branches than in the inlet line in order to maintain a constant total pressure throughout.

Thank you for the response. So essentially, neglecting real world losses, the total pressure is the same no matter where in the system you look. However, the main inlet has a higher dynamic pressure than the branches, and the branches have a higher static pressure than the main inlet. Is this correct?

 

[Rocket Scientist]

Yep.. you got it.

 

[FerPhys]

I believe the pressures would be the same if they're all laying horizontally flat. If the system is set up vertically so that one pipe is higher (relative to the lower pipe) then the pressures would not be the same according to Bernoulli's equation..

 

[OldYat47]

I'll be the devil's advocate for this one. The problem is easily solved. Since there are no frictional losses Pin = P1 = P2 = P3 = atmospheric pressure. Since there is no pressure gradient anywhere all the flow goes straight from Pin to the outlet of P2 due to inertia.

 

[twiz_]

If you imagine there to be a piston in front of the fluid flow in each of the three pipes, it's easy to image that pressure is distributed equally as it is a hydraulic system. Delete the pistons, it technically isn't hydraulic, but it still acts as though.

 

[kingneptune11]

I'll be the devil's advocate for this one. The problem is easily solved. Since there are no frictional losses Pin = P1 = P2 = P3 = atmospheric pressure. Since there is no pressure gradient anywhere all the flow goes straight from Pin to the outlet of P2 due to inertia.

Thanks for the reply.

I believe there is a pressure gradient, though. The outlet is atmospheric pressure, where as P_IN is some value higher than atmospheric pressure. This pressure difference, by definition, creates a pressure gradient, correct?

Thank you.

 

[kingneptune11]

If you imagine there to be a piston in front of the fluid flow in each of the three pipes, it's easy to image that pressure is distributed equally as it is a hydraulic system. Delete the pistons, it technically isn't hydraulic, but it still acts as though.

By distributed equally, do you mean P_IN=P_1=P_2=P_3?

 

[twiz_]

By distributed equally, do you mean P_IN=P_1=P_2=P_3?

Exactly, even if the outlets of each pipe weren't atmospheric pressure, higher or lower, I wouldn't think the pressure would be any different towards the outlet. Is the gradient you're thinking of causing there to be a higher or lower pressure towards Pin? The only difference in pressure I would expect would be from changes in velocity.

 

[Ketch22]

The pressure must be different at the outlets If it is set up as the original drawing. A cross or tee will not evenly distribute unless there is a balancing device on each leg. Then due to the flow carrying directly through from one side to the other the center outlet will flow a higher rate. As a third consideration There is a small but determinable resistance for flow in a pipe. Unless you also balanced the length and bend angles of each leg they will operate at different resistance.
Each of these items contributes to a different flow and pressure.

 

[OldYat47]

The devil's advocate again. You must assume some pressures, some pipe friction characteristics and some fluid properties to work the problem out. If you assume an ideal fluid you still have to come up with a value for supplied pressure and pipe friction. And if all you want is a symbolic solution you still need some pipe friction. IN the real world it takes some force to change the inertia of bits of the fluid stream at the cross. That must be considered also.

 

[wildoats]

I know that this was an old discussion, but in case anyone is around, I am looking at putting three in-line domestic water filters in parallel, to increase the flow rate without significantly affecting the filtration. I recall from studies many moons ago that fluid flows through such splitters in preferential ways, (a phenomenon exploited by fluid logic circuitry) meaning that the flow through each filter could be markedly different, leading to inefficient filtering and premature exhaustion of one or more units. Has anyone an idea of how I might ensure uniform flow through each filter without breaking the bank?

 

[ChemAir]

You may want to start a new thread to get more interest, maybe in the DIY section.

I know that this was an old discussion, but in case anyone is around, I am looking at putting three in-line domestic water filters in parallel, to increase the flow rate without significantly affecting the filtration. I recall from studies many moons ago that fluid flows through such splitters in preferential ways, (a phenomenon exploited by fluid logic circuitry) meaning that the flow through each filter could be markedly different, leading to inefficient filtering and premature exhaustion of one or more units. Has anyone an idea of how I might ensure uniform flow through each filter without breaking the bank?

It's worth being worried about, but in this case, I'm not sure how much real trouble it will cause in this excess capacity case. If one begins to clog, the flow should tend to go to another element, so it is self-regulating to an extent. When the pressure drop increases overall, then all elements need to be changed. The problem will be if one has a breakthrough. I'm not sure how you are monitoring this.

A throttling valve at each filter might control it, but you may have to adjust them pretty regularly as the filters clog, presumably at an uneven rate. The break-the-bank approach would probably be delta P control over each filter, or an externally piloted water pressure regulator (not sure if a reliable one exists) to do this job. These three controls would be in close proximity and cross-talk, so this might be a more daunting application than it seems on the surface. All of these options are counter to wanting to maximize pressure/flow, and they don't address the filter depletion issue if it occurs before clogging.

Since this is somewhat self-regulating, the best you may be able to do without getting nuts is just carefully arranging your piping so it doesn't contribute much to the problem, and leave room to add the throttling valve just-in-case. Three valves rather than one will give you adjustability if you need it.

Is installing a larger filter an option?

 

[wildoats]

Thanks for your prompt reply. You make some good points about the variability of individual filter performance, but it would be hard to measure and control flow rates etc without, as you point out, extra bits 'n pieces. A larger filter would be the logical solution, but I'm really restricted by the space available. This is why I am considering three in-line cartridges, because they can lie horizontally in echelon, taking minimal space and still be accessible for (relatively) easy replacement. I thought Y shaped unions rather than Ts might also reduce turbulence and possible consequent preferred paths, all other things being equal. Another thing might be to swap them out earlier than their theoretical end of life.