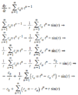1st Order Differential Equation - Power Series Method

In summary, the conversation discussed finding a solution for a differential equation, specifically the equation ##x = x_{HOM} + x_{Inhom}##. The solution was simplified by writing ##sin(t)## as ##\sum_{0}^{\infty}\frac{(-1)^n t^{2n+1}}{(2n+1)!}## and considering solutions for which the sum is always equal to zero. However, it was mentioned that the solution ##c_0 = -t \cdot sin(t)## may not be correct.
  • #1
NicolaiTheDane
100
10

Homework Statement


upload_2018-10-26_11-27-21.png

The Attempt at a Solution


upload_2018-10-26_11-28-2.png


I have deliberately made several obvious steps, because I keep ending up here. However I have no idea what to do from here. I thought about the fact, that differential equations have the solution ##x = x_{HOM} + x_{Inhom}##, but the ##x_{HOM}## ends up the same, except equal 0, which suggests that the only solution is ##c_0 = -t \cdot sin(t)##. as all ##c_n=0, n \geq 1, t \in (0,\infty)##. But that can't be right, because that actually constitute a solution?
 

Attachments

  • upload_2018-10-26_11-27-21.png
    upload_2018-10-26_11-27-21.png
    4.4 KB · Views: 563
  • upload_2018-10-26_11-28-2.png
    upload_2018-10-26_11-28-2.png
    3.5 KB · Views: 578
Physics news on Phys.org
  • #2
try writing ##sin(t)## as ##\sum_{0}^{\infty}\frac{(-1)^n t^{2n+1}}{(2n+1)!}##, simplify the expression and then try to find solutions for which the sum is always going to equal to zero
 

FAQ: 1st Order Differential Equation - Power Series Method

What is the Power Series Method for solving 1st Order Differential Equations?

The Power Series Method is a technique used to solve 1st Order Differential Equations that cannot be solved by traditional methods. It involves expressing the solution as a series of terms, with each term containing increasingly higher powers of the independent variable.

When is the Power Series Method typically used?

The Power Series Method is typically used when the coefficients in the differential equation are not constant or are difficult to work with. It is also useful when trying to find a general solution to a differential equation, as it can produce a series that converges to the solution for a wide range of initial conditions.

What are the steps involved in using the Power Series Method for solving a 1st Order Differential Equation?

The steps for using the Power Series Method are as follows:
1. Assume the solution is in the form of a power series.
2. Substitute the power series into the differential equation and equate coefficients of like powers of the independent variable.
3. Solve for the coefficients by setting up a system of equations.
4. Use the initial conditions to determine the values of the coefficients.
5. Substitute the coefficients back into the power series to obtain the final solution.

What are the advantages of using the Power Series Method?

The Power Series Method is advantageous because it can be used to solve a wide range of 1st Order Differential Equations, including those that cannot be solved by traditional methods. It also provides a general solution that can be used for different initial conditions. Additionally, it allows for easy approximation of the solution by using only a finite number of terms in the series.

Are there any limitations or drawbacks to using the Power Series Method?

There are a few limitations to using the Power Series Method. It requires a certain level of mathematical knowledge and understanding to set up and solve the system of equations. It also may not work for all types of 1st Order Differential Equations, particularly those with singularities or discontinuities. Additionally, the series may not converge for certain initial conditions, making the solution invalid in those cases.

Similar threads

Reduction of order for Second Order Differential Equation
Replies
2
Views
717
Use Wronskian method in solving the given second order differential equation
Replies
7
Views
471
Given unit impulse response, obtain differential equation
Replies
7
Views
967
Differential equation with power series method
Replies
4
Views
1K
Differentiating a power series
Replies
4
Views
1K
Solutions of first-order matrix differential equations
Replies
5
Views
1K
On pointwise convergence of Fourier series
Replies
3
Views
1K
On the ratio test for power series
Replies
2
Views
1K
Solving system of differential equations using elimination method
Replies
10
Views
896
Prove that solutions to autonomous first order DE can't have local maxima
Replies
2
Views
845

Hot Threads

Recent Insights

Back
Top