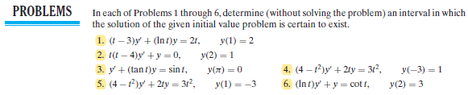karush
Gold Member
MHB
- 3,240
- 5
View attachment 8690
doing #1
ok first I divided thru
$$y' + \frac{\ln{t}}{t-3}y=\frac{2t}{t-3}$$
but the $$\exp\int p(t) \, dt$$ step kinda baloated?
ok I see the denominator has $t-3$ so presume 3 is one of the interval ends
but why 0. ?
book answwer is
View attachment 8691
doing #1
ok first I divided thru
$$y' + \frac{\ln{t}}{t-3}y=\frac{2t}{t-3}$$
but the $$\exp\int p(t) \, dt$$ step kinda baloated?
ok I see the denominator has $t-3$ so presume 3 is one of the interval ends
but why 0. ?
book answwer is
View attachment 8691