york
- 10
- 0
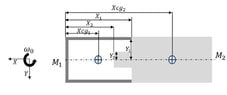
M1 and M2 are rigid bodies that connected. they spin freely around the Z-axis. At a certain time (we will set t=0) when the bodies are in the state described below, the bodies disconnect from each other when each of the bodies is given a speed addition in the direction of the X(V1 and V2 axis respectively). The separation speed is defined as the Vsep=V1-V2 speed difference. What is the minimum separation speed required in order not to cause no harm between the bodies?