2-Capacitor, 2-Resistor Parallel RC Circuit with Switch

[cep]

Homework Statement

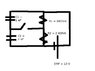
For the attached circuit (which I've drawn rather poorly in GIMP), I need to figure out the charge on each capacitor when the switch has (a) been closed for a long time and (b) been open for a long time.

Homework Equations

Loop and Junction rules, $\Delta$V=IR, C=Q/$\Delta$V, 1/Ceq = 1/C1+1/C2

For charging a capacitor, I = (Vemf/R)e^(-t/RC).

For discharging a capacitor, I = -(Qmax/RC)e^(-t/RC)

The Attempt at a Solution

I think I have a conceptual problem in thinking about where the current goes. I'm inclined to think that there is some sort of equilibrium, where the capacitors can discharge through the smaller circuits while the battery charges them through the larger circuits (both when the switch is open and closed). Can anyone help me think about this problem? Preferably sooner...

Thank you!

-CEP

 

[cep]

Here's the drawing, hopefully, otherwise I can't get the attachment feature to work :/

 

[gneill]

When a DC (battery) powered circuit reaches steady state the current in all capacitors will be zero -- they reach their final charge (voltage) and that's it for them. For all intents and purposes they look like open circuits as far as the rest of the circuit is concerned.

For the closed-switch version of the circuit this means that the voltage drops on the resistors of the circuit are going to determine what the final voltages will be on the capacitors.

For the open-switch case the individual capacitor voltages will depend upon the sequence of events. Is the switch first closed for a long time before being opened, thus starting each of the capacitors off with some initial charge, or are we to assume that the capacitors are initially uncharged and the switch already open when the battery power is first applied? The question doesn't specify one way or the other.