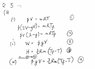unscientific
- 1,728
- 13
Homework Statement
I managed to do part (i) and first part to (ii):
Homework Equations
U = Q + W
The Attempt at a Solution
for the first part:T/Tf = 1/(2 - y)
for (ii):
W = yVP
Given: (3/2)R = Q/(nΔT),
Q = (3/2)nR(ΔT)
Therefore U = Q + W
U = (3/2)nR(ΔT) + yVP
But then,
isn't U already equal to (3/2)nR(ΔT) since its a monoatomic gas?
Then that gives y = 0, so I'm utterly confused.Here's what the answer writes:
W = yVP
H = (3/2)nR(Tf - T) (does H here mean U?)
Does this imply that heat transferred Q, equals to zero? so W = U?
But there's no indication that this is an adiabatic process? How can we assume that?