2 cylinders with rope wrapped around them

[Karol]

Homework Statement

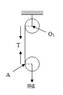
2 identical cylinders of mass m, radius R and moment of inertia I=kmR²are connected with a rope wound around both, according to the drawing. One is falling.
What is the angular acceleration of the upper one?
A hint was given: the acceleration of the lower one is twice the rope's acceleration.

Homework Equations

$$M=I\alpha$$
Steiner's theorem:
$$I_b=I_c+mr^2$$

The Attempt at a Solution

The hint causes me to think the angular acceleration of both cylinders is the same, since the tension T, which rotates them, is the same for both.
The forces that pass through the centers of the cylinders do not have effect on their rotation since they pass through their center of mass, correct? so it leaves the tension T to have the only influence on rotation.
Sum of moments around point A, using Steiner's theorem:
$$mgR=(kmR^2+mR^2)\alpha$$
$$\Rightarrow\alpha=\frac{g}{R(k+1)}$$
But the solution is:
$$\alpha=\frac{g}{R(k+2)}$$

 

[pabloenigma]

for the lower cylinder,we have...

mg-T=ma...I

from the rotation of upper cylinder,

TR=kmR^2$$\alpha$$ (torque eqn)...II


if you have understood the hint...(angular acc is equal for both,and acceleration of lower cylinder is twice that of rope)
also $$\alpha$$R=a/2...
or,...a=2$$\alpha$$R.....III

putting II and III in I,


mg-kmR$$\alpha$$=2mR$$\alpha$$...IV

IV can be solved for $$\alpha$$ to give the required solution



hope that helps...

 

[Karol]

Thanks!