- #1
BunDa4Th
- 188
- 0
Suppose the river is moving east at 4.80 km/h and the boat is traveling Theta = 43.0° south of east with respect to the Earth. You will have to solve two equations and 2 unknowns.
(a) Find the speed of the boat with respect to the Earth. kh/m
(b) Find the speed of the boat with respect to the river if the boat's heading in the water is 60° south of east.
km/h
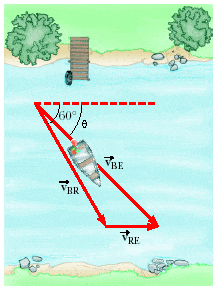
I am having trouble on where to start and what to do. I tried sqrt((4.80(cos43*))^2 + (4.80(sin43*))^2) but still give a wrong answer.
(a) Find the speed of the boat with respect to the Earth. kh/m
(b) Find the speed of the boat with respect to the river if the boat's heading in the water is 60° south of east.
km/h
I am having trouble on where to start and what to do. I tried sqrt((4.80(cos43*))^2 + (4.80(sin43*))^2) but still give a wrong answer.