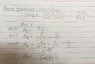yecko said:
Homework Statement
View attachment 222977
Homework Equations
Power series
The Attempt at a Solution
View attachment 222976
As I have to write in form of "x^2n" & "x^2n+1", I am totally have no idea with how can I go on to do the question.
Those I have learned in lecture and online are mostly with only one part of summation... or two parts with two distinctive roots and two constants with it...
Can anyone guide me with what I should do next in order to obtain the answer please? Thank you.
Your posted image is perfectly clear and derives the result more-or-less completely. I can see no way to explain it better than what you are already seeing.
However, I will offer a little hint: If ##y = c_0 + c_1 x + c_2 x^2 + c_3 x^3 + \cdots + c_n x^n + \cdots## then you can write down the series for the left-hand-side of the DE---just do the derivatives and add everything together. The result will have the form ##y'' -5 x y'-5y = D_0 + D_1 x + D_2 x^2 + \cdots ,## where ##D_0, D_1, D_2, \ldots## are combinations of ##c_0, c_1, c_2, \ldots##. Just do some algebra to figure out how the ##D_i## and ##c_j## are related.
However, the result should be ##0## (because ##y## is supposed to solve the DE), so you should have ##D_0 = 0, D_1 = 0, D_2 = 0, \cdots .## That will give you a bunch of equations that relate the different ##c_j## to each other. The two initial conditions give you the rest of the needed information, so you can find all the ##c_j##.
If you cannot see right away how to do the general case (that is, ##D_m## for general, symbolic ##m##) start with writing down all the terms for ##D_m## for ##m = 0,1,2, \ldots, 10,## say, and see what these 11 equations give you. There are no shortcuts---you need to sit down and work it all out.