2nd order ODE circuit, switch question

[kidsasd987]

if we assume the condition immediately after switch is closed (t=0+),

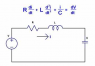
*Capacitor voltage cannot jump.
*Inductor current cannot jump.

dv(0+)/dt=i_c(0+)/c
di(0+)/dt=v_l(0+)/L

which means we can find the initial condition of the post-zero system algebraically.

However, it contradcits to the definition of differentiability since the pre-zero value and post-zero value
of the system are different. (I_c(0+)=/=i_c(0-), v_l(0+)=/=v_l(0-))

I wonder how we can justify the math of the system.
Can I think this as two diffrent systems (ODEs) with one condition shared?

 

[berkeman]

Immediately after the switch is closed, all of the battery voltage appears across the inductor, since there is no current flow in the circuit yet (so no voltage drop across the resistor yet, and the capacitor has not started to charge up yet). Then as current builds in the circuit, the voltage across the inductor falls and more of the voltage appears across the resistor and capacitor. Depending on the component values, there may be some ringing involved, but eventually all of the battery voltage appears across the capacitor, with no current flowing in the circuit.

Does that help?

 

[kidsasd987]

Immediately after the switch is closed, all of the battery voltage appears across the inductor, since there is no current flow in the circuit yet (so no voltage drop across the resistor yet, and the capacitor has not started to charge up yet). Then as current builds in the circuit, the voltage across the inductor falls and more of the voltage appears across the resistor and capacitor. Depending on the component values, there may be some ringing involved, but eventually all of the battery voltage appears across the capacitor, with no current flowing in the circuit.

Does that help?

Oh I understand the physics behind it but what I am confused of is how to interpret the math part.
at t=0, we have different di(0+)/dt and di(0-)/dt values as we consider prezero and postzero conditions. Mathmatically, it contradicts to differentiability.

 

[berkeman]

Oh I understand the physics behind it but what I am confused of is how to interpret the math part.
at t=0, we have different di(0+)/dt and di(0-)/dt values as we consider prezero and postzero conditions. Mathmatically, it contradicts to differentiability.

How do you differentiate a piecewise-continuous function?

 

[meBigGuy]

My math is weak, but I have a problem with you trying to simply differentiate across an instantaneous switch closure (applying a step function) and expecting it to be continuous. (the step function is not continuous at 0)
http://www4.ncsu.edu/~schecter/ma_341_sp06/varpar.pdf

 

[kidsasd987]

How do you differentiate a piecewise-continuous function?

hmm, I thought it was non-differentiable but since it was written as di/dt, I tried to figure out what was going on :)

so, we still write the equation as di/dt, but actually it is non-differentiable? However, the circuit above is written as ODE.

I thought closing switch transforms one system to another, hence changes the initial condition.