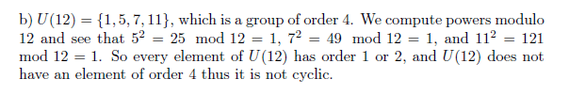karush
Gold Member
MHB
- 3,240
- 5
\nmh{837}
Compute the orders of the following groups: $U(3), U(4), U(12)$ and $U(3), U(5), U(15)$.
On the basis of your answers, make a conjecture about the relationship among $|U(r)|, |U(s)|$, and $|U(rs)|$.
ok I still don't have a clear idea on how to do this $ax=1$
$U(3)=3$
Compute the orders of the following groups: $U(3), U(4), U(12)$ and $U(3), U(5), U(15)$.
On the basis of your answers, make a conjecture about the relationship among $|U(r)|, |U(s)|$, and $|U(rs)|$.
ok I still don't have a clear idea on how to do this $ax=1$
$U(3)=3$
Last edited: