Heloo a_hargy,
Welcome to Physics Forums!
I think I see what's going on. (And RockFreak, I don't think your approach is going to work by itself this time, for reasons I shall describe below).
It's obvious that you have 3 equations and 3 unkowns. But what's not so obvious is that the three equations are not
linearly independent.
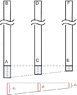
You can see that
\left[ \begin{array}{ccc}0 & 0.4 & 0.8 \\ 0.4 & 0 & -0.4 \\ 0.8 & 0.4 & 0 \end{array} \right] \left[ \begin{array}{c} A \\ C \\ E \end{array} \right] = \left[ \begin{array}{c} 3000 \\ 3000 \\ 9000 \end{array} \right]
But the determinant of the matrix is zero
\left| \begin{array}{ccc}0 & 0.4 & 0.8 \\ 0.4 & 0 & -0.4 \\ 0.8 & 0.4 & 0 \end{array} \right| = 0
The matrix has no inverse. Which indicates that the equations that you chose are not linearly independent of one another. You need some other equation to solve this problem that is linearly independent of the other two.
It turns out that you can throw away anyone of the original equations, and the other two are linearly independent of each other. But you will still need a new third equation (more on that below)
Just a example of what linearly independent means. Suppose we have the equation,
x + y = 1
and we need another equation to solve for
x and
y. Well we could just say,
2x + 2y = 2
That gives us 2 equations and 2 unkowns, so we can solve for
x and
y right? Wrong. The equations are not linearly independent. The second is just the first, multiplied by 2. [Edit: By that I mean that the second equation gives no
new information, that is not already present in previous equations.]
Anyway, back to problem of this thread. Throw away one of the three equations you have now. You'll need to find a new third. And don't bother taking the moment around some different point, because that won't help either this time. But there is an easy equation that you may have forgotten to use, that doesn't have anything to do with moments (Hint: what is the sum of A, C and E?

)