karush
Gold Member
MHB
- 3,240
- 5
$\tiny{311.1.5.19}$
find the parametric equation of the line through a parallel to b.
$a=\left[\begin{array}{rr}
-2\\0
\end{array}\right],
\, b=\left[\begin{array}{rr}
-5\\3
\end{array}\right]$
ok I know this like a line from 0,0 to -5,3 and $m=dfrac{-5}{3}$
so we could get line eq with point slope formula
but this is be done by parametric eq
this was book section I tried to follow..
anyway...
$x=a+tb=
\left[\begin{array}{rr}
-2\\0
\end{array}\right]+t
\left[\begin{array}{rr}
-5\\3
\end{array}\right]$
maybe
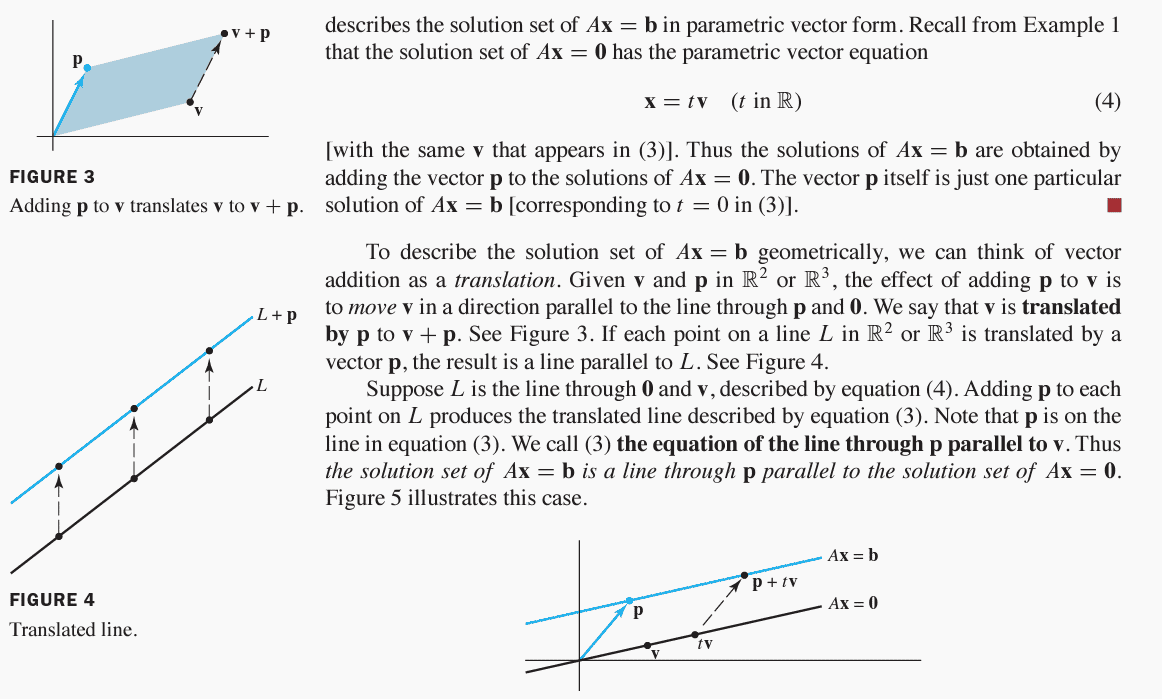
find the parametric equation of the line through a parallel to b.
$a=\left[\begin{array}{rr}
-2\\0
\end{array}\right],
\, b=\left[\begin{array}{rr}
-5\\3
\end{array}\right]$
ok I know this like a line from 0,0 to -5,3 and $m=dfrac{-5}{3}$
so we could get line eq with point slope formula
but this is be done by parametric eq
this was book section I tried to follow..
anyway...
$x=a+tb=
\left[\begin{array}{rr}
-2\\0
\end{array}\right]+t
\left[\begin{array}{rr}
-5\\3
\end{array}\right]$
maybe
Last edited: