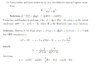Inverting Laplace Transform: Y to f - Explained Steps

[adamwitt]

Ok, so I have uploaded/attached the question and the solution. I just need help understanding the solution please. I understand how to calculate the initial inverse transform, but I included it as the reference to the second part of the question regarding the y'' + 4y' = H(t-3)

Can someone please explain the full steps to invert the laplace transform Y to f, like the solution shows in the last step?
I have got to the following point, but I think I may be forgetting some Laplace Transform identities needed to make my life easier?

I can split the equation into parts where I recognise a few Laplace Transforms but not sure about the rest, cheers...

Y(s) = (1/s).e^-3s.[1/(s²+2²)] + [s/(s²+2²)] - [2/s²+2²]I recognise a few inverse laplace transforms there but without adding my confusion to the mess can someone please clarify how they got the answer? many thanks in advance.
hopefully I didnt make this post toooo convoluted with my thoughts!

 

[icystrike]

U are confused because they have skipped a step.

I bet u must have recognised this part: [s/(s2+22)] - [2/s2+22]

For this part: (1/s).e-3s.[1/(s2+22)] :
(1/(s(s²+2²)))
=(1/4)((1/s)-(s/(s²+2²)))
=(1/4)(H(t-3)-cos(2(t-3)))

 

[adamwitt]

U are confused because they have skipped a step.

I bet u must have recognised this part: [s/(s2+22)] - [2/s2+22]

For this part: (1/s).e-3s.[1/(s2+22)] :
(1/(s(s²+2²)))
=(1/4)((1/s)-(s/(s²+2²)))
=(1/4)(H(t-3)-cos(2(t-3)))

How did you get rid of the e^(-3s) ?

thanks for helping.

 

[icystrike]

You are most welcome adam :)

L^{-1}(e^{-cs}F(s))=f(t-c)
Given :
L^{-1}(F(s))=f(t)