eehsun
- 9
- 0
Hi everyone,
I encountered a problem as a part of the solution of which I needed to get the i-V relation across a solenoid to gain some intution in the other parts of the problem, which is the well known expression
VL=LdiL/dt, where V and i are referenced with respect to the passive sign convention.
Nothing tricky here, just basic stuff - however I wanted to quickly verify this before I moved on in the problem. The following is a simple MSpaint sketch that I have just created for illustrative purposes
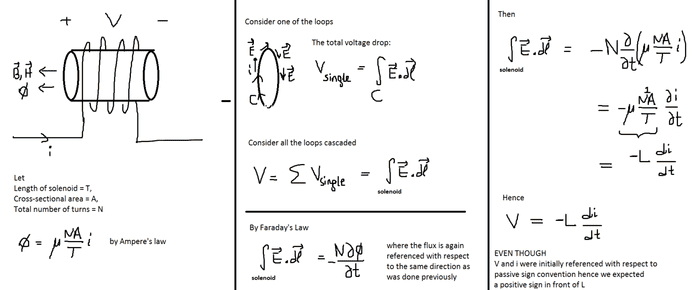
The rest of the details are in the above picture. The question I had in mind is why I am not able to derive the simple relation VL=LdiL/dt for an inductor (solenoid in this case), even though I referenced everything in line with the passive sign convention?
Thanks!
I encountered a problem as a part of the solution of which I needed to get the i-V relation across a solenoid to gain some intution in the other parts of the problem, which is the well known expression
VL=LdiL/dt, where V and i are referenced with respect to the passive sign convention.
Nothing tricky here, just basic stuff - however I wanted to quickly verify this before I moved on in the problem. The following is a simple MSpaint sketch that I have just created for illustrative purposes
The rest of the details are in the above picture. The question I had in mind is why I am not able to derive the simple relation VL=LdiL/dt for an inductor (solenoid in this case), even though I referenced everything in line with the passive sign convention?
Thanks!
Last edited: