Gobil
- 59
- 0
hi All,
I recently got interested in a general solution to diffraction from an object at verious distance and wavelengths. I came across the Fresnel Kirchoff formula (attached formula from Schnars, digital holography).
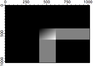
My problem is I cannot seem to replicate a diffraction that makes sense to me from this formula. My approach is to calculate numerically the terms inside the double integral, then integrate in x and y, and display the magnitude squared. If I try this with a square aperture centered in a opaque screen, I get something that looks like the image attached.
Am I doing something basic wrong?
Thanks in advance!
I recently got interested in a general solution to diffraction from an object at verious distance and wavelengths. I came across the Fresnel Kirchoff formula (attached formula from Schnars, digital holography).
My problem is I cannot seem to replicate a diffraction that makes sense to me from this formula. My approach is to calculate numerically the terms inside the double integral, then integrate in x and y, and display the magnitude squared. If I try this with a square aperture centered in a opaque screen, I get something that looks like the image attached.
Am I doing something basic wrong?
Thanks in advance!