A aerialist on a high platform holds on to a trapeze attached to a sup

  • Thread starter Thread starter cmkc109
  • Start date Start date
  • Tags Tags
    Platform
AI Thread Summary
The discussion focuses on calculating the angle θ that a trapeze cord makes with the vertical when an aerialist swings down and releases the trapeze. The initial setup involves an 8.2-meter cord making a 39.8-degree angle with the vertical before the jump. The user attempts to understand the geometry involved, particularly the positions of the aerialist and the trapeze at different points in the swing. Confusion arises regarding the correct interpretation of the lengths and angles involved, particularly in relation to the vertical position of the cord. Clarification is sought on the initial position and the calculations related to the triangles formed in the scenario.
cmkc109
Messages
103
Reaction score
0

Homework Statement



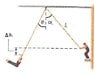
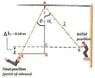
A aerialist on a high platform holds on to a trapeze attached to a support by a 8.2-m cord. Just before he jumps off the platform, the cord makes an angle α of 39.8deg with the vertical. He jumps, swings down, then back up, releasing the trapeze at the instant it is 0.64 m below its initial height. Calculate the angle θ that the trapeze cord makes with the vertical at this instant.

Homework Equations



cos(theta) = A/H

The Attempt at a Solution



So I found the solution online.
8.2 cos 39.8 = 6.3
6.3 + 0.64 =6.94
cos ^-1 (6.94 / 8.2) = 32.2 deg

However I am not understanding it at all. I don't understand where is the initial position, when the rope is vertical or when the guy is holding on to it?
I have attached the picture , can someone label on the picture or explain it please?

My understanding is, the middle is 8.2m , the right rope is 6.3m, and the left rope is 6.94m
but then the calculation doesn't really make sense.
since if the middle is 8.2, to find l, u should do cos 39.8 = 8.2 / l, and l will be 10.67 instead.
 

Attachments

  • swing.jpg
    swing.jpg
    8.8 KB · Views: 2,394
Physics news on Phys.org
The length of the rope is ##l## = 8.2 m. The length of the rope does not change.

Examine some of the triangles shown in the attached figure.
 

Attachments

  • Trapeze.jpg
    Trapeze.jpg
    11.9 KB · Views: 3,125
Last edited:
very helpful, thank you very much.
 
Thread 'Variable mass system : water sprayed into a moving container'

Thread 'Variable mass system : water sprayed into a moving container'

Starting with the mass considerations #m(t)# is mass of water #M_{c}# mass of container and #M(t)# mass of total system $$M(t) = M_{C} + m(t)$$ $$\Rightarrow \frac{dM(t)}{dt} = \frac{dm(t)}{dt}$$ $$P_i = Mv + u \, dm$$ $$P_f = (M + dm)(v + dv)$$ $$\Delta P = M \, dv + (v - u) \, dm$$ $$F = \frac{dP}{dt} = M \frac{dv}{dt} + (v - u) \frac{dm}{dt}$$ $$F = u \frac{dm}{dt} = \rho A u^2$$ from conservation of momentum , the cannon recoils with the same force which it applies. $$\quad \frac{dm}{dt}...
View full post »

Thread 'Egg Drop Challenge! Need ideas for winning designs'

I was thinking using 2 purple mattress samples, and taping them together, I do want other ideas though, the main guidelines are; Must have a volume LESS than 1600 cubic centimeters, and CAN'T exceed 25 cm in ANY direction. Must be LESS than 1 kg. NO parachutes. NO glue or Tape can touch the egg. MUST be able to take egg out in less than 1 minute. Grade A large eggs will be used.
View full post »

Similar threads

Swing Higher on Circus Trapeze: Solve Physics Problem
Replies
1
Views
6K

Hot Threads

Recent Insights

Back
Top