- #1
tryingtolearn1
- 58
- 5
- Homework Statement
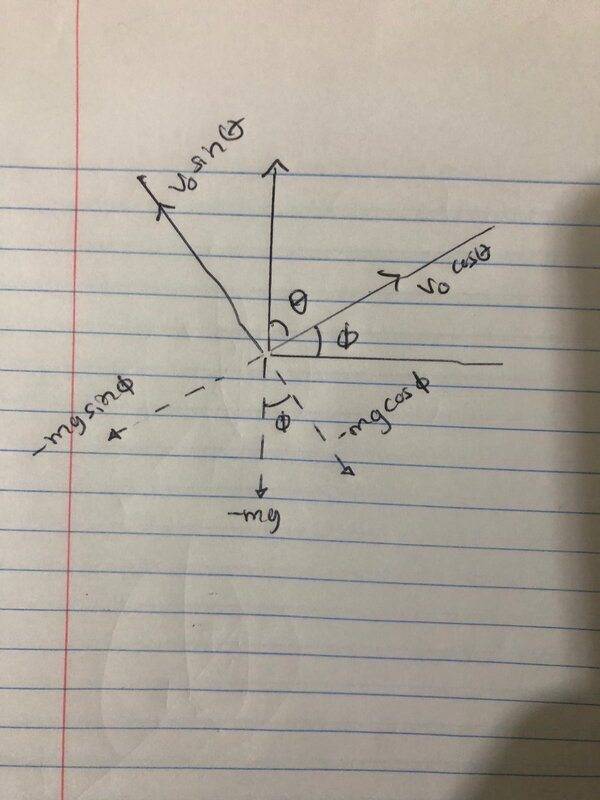
- Suppose a ball is thrown straight up with an initial speed of ##v_i## on an inclined plane, where the plane is inclined at an angle of ##\phi## above the horizontal and the ball's initial velocity is at an angle ##\theta## above the plane.
- Relevant Equations
- ##F=ma##
I understand how the diagram below determined the ##x## and ##y## axis for the velocity vectors but I don't understand the gravity vectors. What I don't understand about the gravity vectors is why is ##-mg## in the ##y-##axis equal to ##-mg\cos\theta## and the ##x-##axis is equal to ##-mg\cos\theta## even though the diagram for the velocity vector has the ##y-##axis as ##v_0\sin\theta## which is exactly on the same axis for the gravity vector so shouldn't the gravity vectors ##\cos## and ##\sin## be flipped? Also, I don't understand how the ##\phi## angle below the horizontal was determined in the diagram. Shouldn't that ##\phi## be instead ##\theta##?