Nickg140143
- 30
- 0
Homework Statement
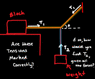
You can find the questions, and relevant diagrams for each within the attached image
Homework Equations
Force Equations
ƩF=ma
f_k=μ_kN
Work Equations
W=Fs
(in this case, s=h)
W_{tot}=\frac{1}{2}mv^2-\frac{1}{2}mv_0^2
My Questions (these are also written on the diagrams):
-Looking at the diagram with the black background, have these tensions been identified correctly? If so, how would I try to solve for T2, given I've created all of my force equations?
-looking at the attachment that has two problems, with forces identified, and specific areas of interest highlighted:
-Have I identified my forces correctly?
-In question 1, it says block m2 just "drops" a distance h, since it says nothing about
the velocity being constant, should I assume that there is an acceleration in the
system?
-In question 2, it says that block c descends with a constant velocity, can I say that
block A and block B also move through the system at a constant velocity?
-When finding the work done on each individual body in both questions, I forgot that
none of the tensions are given to me. Would I simply set up force equations in order
find each tension?
It seems I have most of the concepts understood to a certain degree, but their are certain things that tend to trip me up quite a bit, any help regarding these question would be greatly appreciated.