How Is the Third Answer Calculated in This Lawn Mower Physics Problem?

[justinbaker]

Here is the question i have. I got the first two no prob. But ihave no idea how i got the third answer. The answers shown are all correct. So if anyone can explain how to get the third answer, thanks everyone

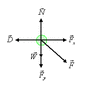
A person pushes a 17.0 kg lawn mower at constant speed with a force of 71.0 N directed along the handle, which is at an angle of = 46.0° to the horizontal

http://www.webassign.net/giancoli5/4_40alt.gif

Calculate the horizontal retarding force on the mower = 49.3 N

Calculate the normal force exerted vertically upward on the mower by the ground =218

Calculate the force the person must exert on the lawn mower to accelerate it from rest to 1.1 m/s in 2.0 seconds (assuming the same retarding force).
=82.8


Thanks,
justinbaker@gmail.com

 

[Leong]

Since the mover moves in the horizontal direction only, we will consider the x-components only. Left direction : Negative; Right direction: Positive.
<br /> \begin{multline*}<br /> \begin{split}<br /> &amp;Newton&#039;s\ 2nd\ Law:\\<br /> &amp;\sum \vec{F}=m\vec{a}\\<br /> &amp;\vec{F_x}+\vec{D}=m\vec{a}\\<br /> &amp;|\vec{F}|cos46^0 + (-49.3)=17.0*(\frac{1.1-0}{2.0})\\<br /> &amp;|\vec{F}|=84.4\ N\\<br /> \end{split}<br /> \end{multline*}<br />

 

[M98Ranger]

The third answer, 82.8 N, can be calculated using Newton's Second Law of Motion, which states that force equals mass times acceleration (F=ma). In this scenario, the mass of the lawn mower is given as 17.0 kg and the acceleration is 1.1 m/s^2. Therefore, the force needed to accelerate the mower can be calculated as 17.0 kg x 1.1 m/s^2, which equals 18.7 kg*m/s^2 or 18.7 N. However, this only accounts for the force needed to overcome the retarding force (49.3 N) and does not take into account the force needed to maintain the constant speed of the mower. So, the total force needed is 49.3 N + 18.7 N, which equals 68.0 N. However, the problem states that the person is pushing with a force of 71.0 N, so the actual force needed to accelerate the mower would be 71.0 N - 49.3 N, which equals 21.7 N. This is the force that the person must exert on the lawn mower to accelerate it from rest to 1.1 m/s in 2.0 seconds. I hope this helps clarify the calculation for you.