A problem involving two velocities (special relativity)

[raul_l]

Hi.

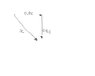
An object is moving at 0.9c toward the y-axis (with respect to reference frame S). What is the velocity of the object with respect to reference frame S' that moves at 0.9c toward the x-axis?

I get the right answer if I assume that the Lorentz factor of the object moving with respect to S' is the product of the Lorentz factor of S' and that of the object moving with respect to S. In other words
\frac{1}{\sqrt{1-\frac{x^2}{c^2}}}=\frac{1}{1-\frac{0.9^2}{c^2}}
in which case x=0.98c which should be correct.

However, I have no idea what I'm doing here so any guidance would be appreciated.

 

[OlderDan]

An object is moving at 0.9c toward the y-axis (with respect to reference frame S). What is the velocity of the object with respect to reference frame S' that moves at 0.9c toward the x-axis?

Did you state this problem correctly? It is unusual to say S' is moving in the y direction (toward the x-axis). If the statement is correct S' and the object are moving at right angles in S.

 

[raul_l]

Well, this is what I meant. (see the drawing).

(and sorry, if I didn't translate the problem into english correctly)

 

[OlderDan]

Well, this is what I meant. (see the drawing).

(and sorry, if I didn't translate the problem into english correctly)

OK I see that you really do have a particle moving through S in a direction perpendicular to the motion of S' in S.

I really do not see how you did your computation in the original post. Your diagram does not seem to incorporate the things you need to recognize to do this problem. In particular, if your diagram is drawn in S', the horizontal velocity component is altered by the time dilation effect, while the vertical component is not. The particle moves the same horizontal distance in both frames, but time dilation results in a lower velocity in S' than observed in S. Since the particle has no vertical motion in S, its vertical velocity in S' is v, the speed of S' relative to S.

The horizontal component would be 0.9c*sqrt(1-v^2/c^2), while the vertical compoent would be 0.9c. Adding these components gives a velocity of magnitude of .982c

The general approach to this kind of additiuon is outlined here.

http://panda.unm.edu/courses/finley/P262/relativity/relativity.html

See especially equations (7) and (8) that tell you how to deal with parallel and perpendicular (to the relative motion of the frames) velocity components. If you apply those equations correctly, they will reduce to what I described above.