Ryker said:
Yeah, I'd be grateful for that simpler method, if you're willing to share it with me :) ?
Of course. :) Sorry for not replying to this yesterday.
One general idea to keep in mind in statics problems such as this is that you can always relate forces to one another by one of two methods:
- You can say that the sum of all the forces acting on a body, resolved in a certain direction, is equal to zero. For n forces this gives an equation something like:
F_1 + F_2 + ... + F_n = 0
possibly with some sines or cosines in the expression for each force, if there's angles involved.
- We can also say that the sum of all the moments acting on the body around a point are zero. This gives an equation something like:
F_1d_1 + F_1d_2 + ... + F_nd_n = 0
Where the forces F are as above and the d's are the perpendicular distances (with either a positive or negative sign - decide in advance which direction will be positive, and stick to it) from where each force acts to the point we're taking moments around. Note that we can take moments around any point on or off the object, and they should sum to zero as long as the object is static.
These two ideas are actually enough to solve almost any statics problem of this type, as long as you're willing to do some algebra. I'll use your problem of the ball on the two scales to illustrate.
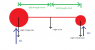
Oh, and refer back to my rubbish mspaint sketch in my last post :)
I'll call our 'reaction' forces from each scale R_1 and R_2. Since if we take moments about a point that a force passes through, we get an equation without that particular force in it, I'm going to make two equations by taking moments about the points at which each reaction force acts on the ball. So firstly, for the left (bigger) ball, we're going to get an equation that says:
moment from weight of rod + moment from weight of small ball - moment from R2 = 0
Notice the minus sign, since the force R2 acts in the opposite direction to the others. Using the numbers you gave originally, noting that force due to gravity is 9.81 ('g') Newtons per kilogram of mass, this gives:
9.81 \times 1kg \times 0.5m + 9.81 \times 2kg \times 1m - R_2 \times 1m = 0
Rearranging and solving for R_2 gives:
R_2 = 9.81 \times 2.5 N
Doing exactly the same thing on the other side (moments around small ball) gives:
moment from weight of rod + moment from weight of large ball - moment from R1 = 0
hence:
9.81 \times 1kg \times 0.5m + 9.81 \times 4kg \times 1m - R_1 \times 1m = 0
so:
R_1 = 9.81 \times 4.5 N
Now consider our scales. The forces acting upon them are equal (by Newton's 3rd law) to R1 and R2. If they give a reading in kilograms then we are going to lose the factors of 9.81 above, so the scale under the heavy ball will read 4.5kg, and that under the light ball will read 2.5kg.
Notice that these add to 7kg, which is the mass of the whole system, as we would hope. :)
Alternatively we could have used the fact that the forces must all add to zero to get a different equation above, and we could have taken our moments about the centre of gravity, but we would have to solve simultaneous equations then (since both equations would have had both R1 and R2 in them). We would get the same answer.
I hope this is clear. I've deliberately made this a lot more long-winded than it needs to be, so my apologies if it was a bit dull, but I was just trying to explain everything as fully as possible. :)