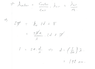A rope of mass m and length L is hanging from the ceiling.

[Natchanon]

Homework Statement

Part C: Find fundamental frequency.

Homework Equations

Tension(y) = μgy
v(y) = sqrt(gy)
Time it takes to travel from bottom to top = t_up = 2srqt(L/g)

The Attempt at a Solution

I found part A and B, which are tension and velocity. I don't know how to find part C because velocity isn't constant so I can't just use f = (1/2L)sqrt(gy). I thought period was 2t_up, but that's wrong. The period is 4t_up, which I don't understand why. When the wave pulse reaches the ceiling, it changes phase and bounces back down, then it bounces up again with the same phase, then it changes phase to the same phase as the original pulse. Is that why we say period is 4t_up? When it comes back to the starting position with the same phase as the first incident wave?[/B]

 

[haruspex]

The period is 4t_up, which I don't understand why.

I see this is marked as solved. In the absence of an explanation for that I assume it is a mistake.

the difficulty is in relating, one the one hand, the traveling of a wave pulse from one end to the other to, on the other hand, an initial and final configuration of the rope.
In the simplest oscillation mode, the rope will be at one time straight and vertical, at another, forming an arc with no inflection points from its attachment at the ceiling to the lower end, that lower end being at its maximum deviation. How do you think those two states relate to t_up?

 

[Natchanon]

I see this is marked as solved. In the absence of an explanation for that I assume it is a mistake.

the difficulty is in relating, one the one hand, the traveling of a wave pulse from one end to the other to, on the other hand, an initial and final configuration of the rope.
In the simplest oscillation mode, the rope will be at one time straight and vertical, at another, forming an arc with no inflection points from its attachment at the ceiling to the lower end, that lower end being at its maximum deviation. How do you think those two states relate to t_up?

Because it is a free end, arc is 1/4 of the wavelength? L = λ/4 ==> λ = 4L.

 

[haruspex]

Because it is a free end, arc is 1/4 of the wavelength? L = λ/4 ==> λ = 4L.

That is certainly true. But is it obvious how that relates to the wave speed?

 

[Natchanon]

That is certainly true. But is it obvious how that relates to the wave speed?

v = sqrt(gy) = 4L / T ==> T = 4L / sqrt(gy). But v isn't constant because it depends on y. Can I say that it takes 1 t_up to form λ/4, so it must take 4t_up to form λ, which means period = 4t_up?

 

[Natchanon]

v = sqrt(gy) = 4L / T ==> T = 4L / sqrt(gy). But v isn't constant because it depends on y. Can I say that it takes 1 t_up to form λ/4, so it must take 4t_up to form λ, which means period = 4t_up?

Then I'll use period = 4t_up to find the fundamental frequency.

 

[haruspex]

Can I say that it takes 1 t_up to form λ/4

I think so, I was just saying it is not quite obvious.

 

[Natchanon]

My instructor said "The key concept here is that resonances if fundamentally a phenomenon of constructive interference. Think the guy in the kiddie pool video we saw in class, building a big wave by sending out waves that bounced off the edge of the pool and came back to the center, and then building by sending a new wave each time." I'm not sure how this applies here. I know that if we send a wave with the same phase as the reflected wave, we'll have one huge amplitude wave covering the entire length of the rope.