bolzano95
- 89
- 7
Lets say we have a system of two point particles (1. and 2.) which are rotating around an axis.
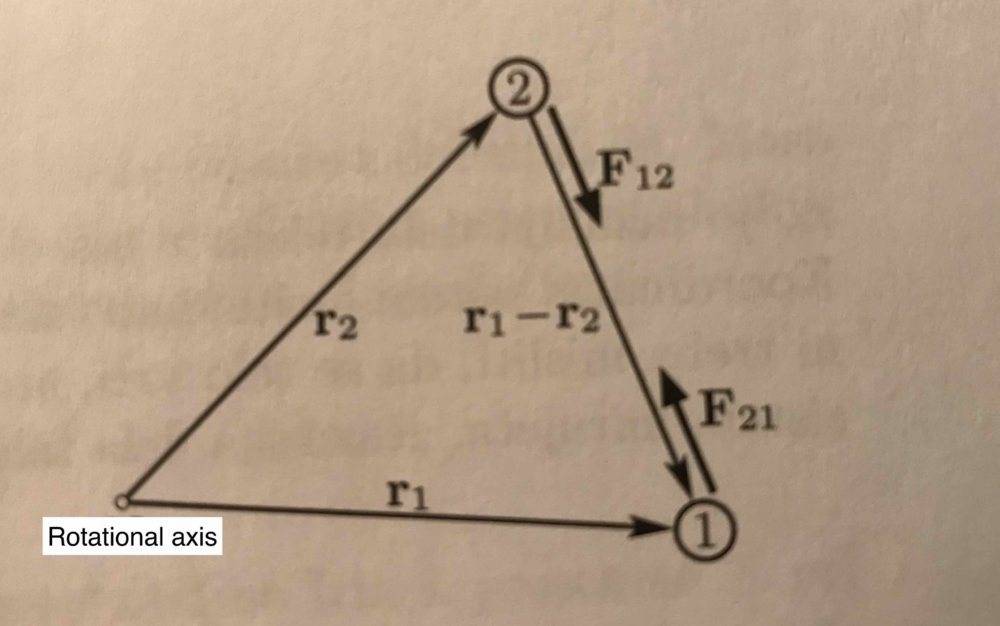 What is written next in my physics course book is: The torque of a 2.body on the 1. body is M21=r1xF21 and the torque of the 1.body on the 2.body is M12=r2xF12. Understandable.
What is written next in my physics course book is: The torque of a 2.body on the 1. body is M21=r1xF21 and the torque of the 1.body on the 2.body is M12=r2xF12. Understandable.
But how? There is no mention or suggestion that those two particles are attracted each other.
I don't understand why are we having inner torques in this example- we are dealing with a system: and it's normal that the inner forces cancel each other out based on the 3rd Newtons Law.
So why are we dealing with inner torques?
I think it's useless thinking about inner torques in the system: if we divide a rigid body to tiny pieces and we take them as point particles, the sum of inner torques is 0.
But the author is trying to derive a general equation for a rotating system of point particles and a rigid body. But he starts explaining the theory in such a confusing way that I'm not sure what I'm missing.
But how? There is no mention or suggestion that those two particles are attracted each other.
I don't understand why are we having inner torques in this example- we are dealing with a system: and it's normal that the inner forces cancel each other out based on the 3rd Newtons Law.
So why are we dealing with inner torques?
I think it's useless thinking about inner torques in the system: if we divide a rigid body to tiny pieces and we take them as point particles, the sum of inner torques is 0.
But the author is trying to derive a general equation for a rotating system of point particles and a rigid body. But he starts explaining the theory in such a confusing way that I'm not sure what I'm missing.